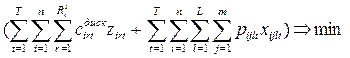Блам Ю.Ш., Машкина Л.В.
Модели
и методы прикладного анализа (производственные системы)
Учебно-методический
комплекс к курсу
Введение.
Раздел «Модели и методы прикладного
анализа (производственные системы)» читается для бакалавров экономического
факультета по направлению «Экономика» (4 курс) и является второй частью общего
курса.
Представленный в данном комплексе
материал условно можно разбить на три части:
· описание
различных типов экономико-математических моделей и некоторые специфические
методы их реализации;
· расчеты в
условиях неопределенности исходной информации и экономико-математический анализ
оптимизационных решений;
· набор конкретных
ситуаций, предлагаемых для самостоятельного моделирования анализа.
Первая часть начинается с анализа
простейших моделей, сводимых к транспортной задаче. Модели оптимизации
производства однородной продукции с учетом грузопотоков при условии линейной
зависимости показателей эффективности плана от объемов производства и перевозок
могут строиться на основе открытой транспортной задачи линейного
программирования. Это позволяет одновременно с формированием оптимального плана
перевозок решать проблему размещения производства путем отбора лишь некоторых
предприятий-поставщиков из числа заданных. Модификации модели позволяют
учитывать многоэтапность производства, резервирование мощностей, складирование
и т.п. Однако вследствие упрощенного описания производственных возможностей
транспортные задачи редко находят применение при решении сложных экономических
задач и используются как блоки в системах моделей.
Далее рассматриваются производственные и
производственно-транспортные модели в «дискретной» и «непрерывной» постановке.
Дискретные производственные модели описывают экономический
процесс в виде альтернативных вариантов развития производственных
объектов, из множества которых требуется выделить оптимальный (в смысле
заданного критерия эффективности) набор, удовлетворяющий заданным ограничениям.
«Непрерывные» модели позволяют представить более широкую область вариации, но
существенно используют линейность зависимости показателей, описывающих
производственные возможности. Эти же замечания относятся и к группе
динамических моделей.
Экономический
процесс
является управляемым, если можно влиять на ход его развития. Под управлением
понимается совокупность решений, принимаемых на каждом этапе для влияния на ход
развития процесса. В качестве метода оптимизации и иллюстрации логики принятия
многошаговых решений приведен метод динамического программирования - метод
рекуррентных соотношений, который основывается на использовании принципа
оптимальности, разработанного американским математиком Р. Беллманом.
В условиях неопределенности исходной
информации (особенно, об условиях функционирования объектов в прогнозируемом
периоде) необходимо принимать управленческие решения, с учетом возможной вариации
условий реализации принятого решения. Такого рода модели и методы их реализации
представлены во второй части. Здесь же дается экономическая интерпретация
двойственных переменных и элементов обратной матрицы к базису оптимального
решения линейно-программных моделей.
Методические материалы по разделу курса
«Модели и методы прикладного анализа (производственные системы)» в виде
печатных учебных пособий в таком виде еще не издавались. В представляемом
УМК содержание разделов обновлено и приведено в соответствие с требованиями
образовательного стандарта РФ и включает более широкий перечень видов
самостоятельных исследовательских работ и контроля знаний, с возможностью
использования автоматизированного контроля.
Предлагаемое пособие «Модели и методы
прикладного анализа (производственные системы)» позволит бакалаврам более
рационально организовать индивидуальный познавательный процесс, а
преподавателям – более продуктивно и творчески проводить семинарские занятия.
Авторы особо признательны Ершову Юрию Семеновичу за предоставленные материалы
по моделям транспортного типа, а также Барабашу Сергею Борисовичу за
комментарии по использованию MS Excel.
ТРАНСПОРТНЫЕ
ЗАДАЧИ
Транспортные задачи – частный случай
задач математического (линейного) программирования, многообразие их постановок
и методы решения изложены в соответствующей математической литературе. Различают
два вида математических транспортных задач – в виде “шахматки” и в сетевой
постановке. В задачах шахматного типа
все ненулевые коэффициенты каждой строки исходной матрицы симплекс-таблицы
имеют один и тот же знак, в задачах в сетевой постановке в матрице существуют
строки, в которых встречаются как положительные, так и отрицательные ненулевые
коэффициенты.
Слово “транспортная” не означает, что
такие задачи могут использоваться только для оптимизации перевозок, такое
название они получили просто потому, что задачи нахождения оптимальных по
критерию минимизации суммарных транспортных затрат схем
прикрепления потребителей к поставщикам исторически были первыми в
совокупности различных экономических проблем, решаемых с помощью моделей такого
вида.
Наиболее популярной является следующая
постановка математической транспортной задачи в виде «шахматки»:
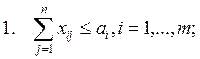
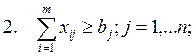
![]()
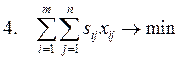
где
xij - искомые
объемы перевозок продукции из пункта i в
пункт j; ai - наличие
продукции в пункте i (называемом
обычно пунктом производства); bj - спрос на продукцию в j-м пункте потребления; sij - удельные (т.е. в расчете на единицу
продукции) затраты на доставку продукции из пункта i в пункт j.
Если в ограничениях 1. правые и левые
части умножить на “
Задача 1. – 4. называется
закрытой транспортной задачей, если 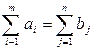 , в этом случае ограничения 1. и 2. выполняются как
равенства на всех допустимых планах. Задача 1. – 4. называется открытой транспортной
задачей, если
, в этом случае ограничения 1. и 2. выполняются как
равенства на всех допустимых планах. Задача 1. – 4. называется открытой транспортной
задачей, если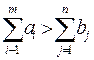 . В этом случае многие алгоритмы решения транспортной
задачи требует ее предварительного сведения к закрытой задаче путем введения
дополнительных переменных. Так как при положительных параметрах sij ограничения 2. на оптимальном плане
всегда выполняются как равенства (что легко доказать от противного), то
дополнительные переменные вводятся только в ограничения 1., которые в
результате принимают вид
. В этом случае многие алгоритмы решения транспортной
задачи требует ее предварительного сведения к закрытой задаче путем введения
дополнительных переменных. Так как при положительных параметрах sij ограничения 2. на оптимальном плане
всегда выполняются как равенства (что легко доказать от противного), то
дополнительные переменные вводятся только в ограничения 1., которые в
результате принимают вид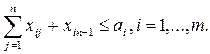 По аналогии переменные xin+1 называют
поставками в (n+1)-й, фиктивный пункт потребления.
Однозначно определяется и сумма дополнительных переменных:
По аналогии переменные xin+1 называют
поставками в (n+1)-й, фиктивный пункт потребления.
Однозначно определяется и сумма дополнительных переменных: 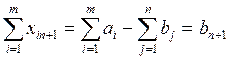 .
.
В результате сведенная к закрытой
транспортная задача будет иметь следующий вид:
1а.
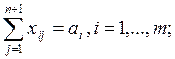
2а.
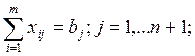
3а.
![]()
4а.
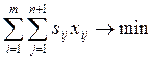
Коэффициенты sin+1 целевой функции
равны нулю. Единственное, достаточное и необходимое, условие разрешимости
задачи 1. – 4.: 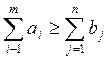 . Этим транспортная задача выгодно отличается от задач
линейного программирования общего вида, где чаще всего факт отсутствия
оптимального или просто допустимого решения устанавливается уже в процессе
поиска и улучшения допустимого решения.
. Этим транспортная задача выгодно отличается от задач
линейного программирования общего вида, где чаще всего факт отсутствия
оптимального или просто допустимого решения устанавливается уже в процессе
поиска и улучшения допустимого решения.
Для решения транспортной задачи
1а. – 4а. используется более простой по сравнению с универсальным
симплекс-методом метод потенциалов. Возможность его применения обусловлена
сравнительной легкостью построения первоначального допустимого плана (например,
методом северо-западного угла) и нахождения решения соответствующей ему системы
уравнений двойственной задачи, поскольку в транспортной задаче это решение
находится с точностью до постоянного слагаемого (одну из переменных
двойственной задачи можно задать произвольно, остальные последовательно
вычисляются из уравнений двойственной задачи).
Напомним суть метода потенциалов на
конкретном числовом примере.
Пусть
a = (50, 75,100,
120); b
= (40, 80, 110, 70), а матрица {sij}:
|
3 |
5 |
4 |
6 |
|
2 |
4 |
1 |
5 |
|
8 |
3 |
2 |
4 |
|
2 |
5 |
6 |
1 |
Задача
оказалась открытой, предложение (345) превышает спрос (300) на 45 единиц, поэтому вводим фиктивный пункт
потребления с объемом потребления b5 = 45.
В этой шахматной таблице (в левом
верхнем углу клеток стоят величины sij) приведено
первоначальное базисное решение, полученное методом "северо-западного
угла», и соответствующее этому базису, решение системы уравнений двойственной
задачи: vj –
ui =
sij для всех базисных xij
|
b a |
40 |
80 |
110 |
70 |
45 |
|
|
50 |
3 40 |
5 10 |
4 |
6 |
0 |
0 |
|
75 |
2 |
4 70 |
1 5 |
5 |
0 |
1 |
|
100 |
8 |
3 |
2 100 |
4 |
0 |
0 |
|
120 |
2 |
5 |
6 5 |
1 70 |
0 45 |
-4 |
|
|
3 |
5 |
2 |
-3 |
-4 |
u v |
Переменная ui была задана
равной нулю, остальные последовательно вычислялись по формуле “цена в пункте
потребления равна цене в пункте производства плюс транспортные затраты” –
наличие u1 = 0 сразу
позволяет найти v1 = u1+3 и v2 = u1+5; зная v2, можно найти u2 = v2 – 4. И т.д.
Является ли полученный допустимый план
оптимальным? Признаком оптимальности служит выполнение всех ограничений
двойственной задачи: vj –
ui ≤ sij, для всех i и j.
Для базисных клеток ограничения
двойственной задачи выполняются как равенства, проверка необходима лишь для
небазисных клеток. Рассчитаем невязки по клеткам шахматки, где поставки
нулевые.
Δij = vj – ui – sij, для
всех i и j, где xij = 0.
В
нашей таблице ограничения двойственной задачи не выполняются для переменных x41 и x42. (Δij > 0) Поскольку
нарушение ограничений двойственной задачи максимально для переменной x41, рекомендуется
ввести в базис именно ее. Для определения ее значения и переменной, исключаемой
из базиса, строим цепочку по базисным переменным из “+” и “-“: Помеченные
знаком “+” переменные будут увеличиваться при увеличении значения переменной x41, помеченные
знаком “-“ – уменьшаться.. В результате должны сохраниться балансы по всем
строкам и столбцам.
|
b a |
40 |
80 |
110 |
70 |
45 |
|
|
50 |
3 -
40 |
5 +
10 |
4 |
6 |
0 |
0 |
|
75 |
2 |
4 -
70 |
1 + 5 |
5 |
0 |
1 |
|
100 |
8 |
3 |
2 100 |
4 |
0 |
0 |
|
120 |
2 + |
5 |
6 - 5 |
1 70 |
0 45 |
-4 |
|
|
3 |
5 |
2 |
-3 |
-4 |
u v |
Значение вводимой в базис переменной
будет равно наименьшему значению из переменных прежнего базиса среди помеченных
знаком “-“. В нашем случае переменная x41 войдет в новый
базис со значением “
И это решение еще не оптимально.
Нарушения ограничений двойственной задачи (положительные невязки) имеют место
для переменных x32, x15 и x35.
|
b a |
40 |
80 |
110 |
70 |
45 |
|
|
50 |
3 35 |
5 15 |
4 |
6 |
0 |
0 |
|
75 |
2 |
4 - 65 |
1 + 10 |
5 |
0 |
1 |
|
100 |
8 |
3 + |
2 - 100 |
4 |
0 |
0 |
|
120 |
2 5 |
5 |
6 |
1 70 |
0 45 |
1 |
|
|
3 |
5 |
2 |
2 |
1 |
u v |
|
b a |
40 |
80 |
110 |
70 |
45 |
|
|
50 |
3 -
35 |
5 15 |
4 |
6 |
0 +
|
0 |
|
75 |
2 |
4 |
1 75 |
5 |
0 |
1 |
|
100 |
8 |
3 65 |
2 35 |
4 |
0 |
2 |
|
120 |
2 +
5 |
5 |
6 |
1 70 |
0 -
45 |
1 |
|
|
3 |
5 |
4 |
2 |
1 |
u v |
Осталась
всего одна положительная невязка – ограничения двойственной задачи не
выполняются для переменной x15. После
включения этой переменной в базис (и исключения переменной x11) получаем оптимальное
решение:
|
b a |
40 |
80 |
110 |
70 |
45 |
|
|
50 |
3 |
5 15 |
4 |
6 |
0 35 |
0 |
|
75 |
2 |
4 |
1 75 |
5 |
0 |
1 |
|
100 |
8 |
3 65 |
2 35 |
4 |
0 |
2 |
|
120 |
2 40 |
5 |
6 |
1 70 |
0 10 |
0 |
|
|
2 |
5 |
4 |
1 |
0 |
u v |
Это оптимальное решение не является
единственным, о чем свидетельствует наличие нулевых невязок для небазисных
переменных x13 и x42. Если ввести
любую из них в базис (таким же способом, как это делалось для переменных, на
которых нарушался критерий оптимальности), то можно получить другое решение
прямой задачи с такими же суммарными транспортными затратами. Оптимальными
решениями будут также и все линейные комбинации оптимальных базисных решений
(если X1 и X2 – оптимальные
решения, то оптимальными будут и все решения, полученные по формуле aX1 + (1-a)X2 при условии что
0 ‹ a
‹ 1).
Отметим, что если бы для всех небазисных
клеток ограничения двойственной задачи выполнялись как строгие неравенства, то
в этом случае полученное оптимальное решение было бы единственным.
Полученное одновременно с оптимальным
решением прямой задачи оптимальное решение двойственной не является
единственным – последнее всегда находится с точностью до постоянного
слагаемого. Если все оценки (“потенциалы пунктов производства и потребления”)
увеличить или уменьшить на одно и то же число, то новая совокупность оценок
тоже будет решением двойственной задачи. Среди всех решений двойственной задачи
наибольшую ценность представляет “нормированное” решение – такое, в котором
минимальная из всех переменных равна нулю, а все остальные, соответственно,
неотрицательны. Только нормированные оценки имеют простую экономическую
интерпретацию – они показывают, как изменится значение целевой функции при
изменении на единицу соответствующего элемента вектора правых частей (естественно,
лишь в том случае, если подобные изменения правых частей не приведут к
изменению оптимального набора базисных переменных, т.е. когда полученное
решение имеет область устойчивости). Нормированное решение можно получить, если
сразу решить исходную задачу 1. – 4. как задачу линейного программирования
общего вида (симплекс-методом), не сводя ее предварительно к закрытой постановке:
у всех ограничений, оказавшихся несущественными, т.е. выполняющимися на
оптимальном решении как строгие неравенства, оценки окажутся равными нулю.
В рассмотренном выше примере полученная
на последнем шаге система оценок случайно оказалась нормированной. Если бы это
было не так, то для перехода к нормированной системе необходимо было бы из всех
полученных оценок вычесть значение самой меньшей из них.
Экономический смысл полученных оценок:
они показывают, насколько уменьшатся (увеличатся) суммарные транспортные
затраты при ослаблении (усилении) ограничений 1. (или 2.) на единицу. В нашем
примере оптимальное решение устойчиво (все базисные переменные положительны),
изменение любого из параметров a и b на малую
величину не приводит к смене базиса, поэтому можно утверждать, например, что
если бы значение a2 было равно 76,
то при неизменности всех остальных параметров значение целевой функции на
оптимальном плане было бы меньше на 3 единицы. Напротив, если бы значение b2 возросло на единицу,
то суммарные транспортные затраты увеличились бы на 5 единиц.
Число переменных в базисных решениях
транспортной задачи должно быть равным числу ограничений в задаче 1. – 4. и на
единицу меньше числа ограничений в задаче 1а. – 4а. (суммы числа строк и числа
столбцов шахматной таблицы). Последнее обусловлено тем, что система уравнений
1а. – 2а. линейно зависима, одно (любое) уравнение является следствием из всех
остальных.
Не всегда удается построить такое
решение, в котором все базисные переменные положительны, может оказаться так,
что при построении первоначального плана число положительных xij оказывается меньше необходимого. В этом
случае в число базисных (используемых для расчета потенциалов в «шахматке») необходимо включить недостающее число переменных
с нулевыми значениями. Такие решения называют вырожденными. Выбор включаемых в
число базисных переменных с нулевыми значениями может быть произвольным,
необходимо лишь обеспечить отсутствие циклов (линейной зависимости между
базисными переменными) – невозможность построения замкнутой цепочки из “+” и
“-“ только по базисным переменным. Работа с вырожденными планами практически
ничем не отличается от работы с невырожденными – базисные нули можно
рассматривать как очень малые положительные числа.
В ходе выполнения итераций методом
потенциалов вырожденный план может перейти в невырожденный. Напротив,
изначально невырожденный план может перейти в вырожденный (если среди
помеченных знаком “-“ переменных окажутся две или более с одинаковыми
минимальными значениями, то из базиса может быть исключена лишь одна из них,
остальные остаются в числе базисных с нулевыми значениями).
На трудоемкость расчетов вырожденность
планов не оказывает влияния. Но в случае вырожденности оптимального плана и
наличия множественности (по набору базисных переменных) оптимальных решений для
некоторых из них могут получаться разные решения двойственных задач
(множественность оптимальных планов в случае отсутствия среди них вырожденных
не сопровождается множественностью решений двойственной задачи – решение
последней, с точностью до постоянного слагаемого, будет единственным). Главная
неприятная для целей экономического анализа особенность вырожденных планов –
отсутствие области устойчивости, малые изменения некоторых из параметров a и (или) b могут привести
к изменению набора переменных оптимального базиса и к другому решению
двойственной задачи.
Далеко не всегда пригодна универсальная
постановка математической транспортной задачи, не требующая какой-либо
дополнительной работы с информацией. В частности, исходной проблемой может быть
не минимизация суммарных транспортных затрат, а максимизация прибыли от
выполнения перевозок – в качестве параметров sij в этом случае
будет удельная (в расчете на единицу перевозимого продукта) прибыль из каждого
пункта производства в каждый пункт потребления. Для того, чтобы перейти к
стандартной постановке на минимум значения целевой функции и не изменять
алгоритм решения, в этом случае достаточно поменять знаки коэффициентов целевой
функции на противоположные.
Далее, между некоторыми пунктами
производства и пунктами потребления связь может отсутствовать (в исходной
задаче набор переменных xij не является полным,
их количество меньше произведения m*n). При ручном счете иногда достаточно исключить
соответствующие клетки шахматной таблицы из числа используемых при построении
первоначального плана и при последующей проверке для небазисных переменных
выполнения ограничений двойственной задачи. При реализации на ЭВМ, а также при
затруднениях при построении первоначального плана (не удается сразу его
построить, не используя клетки таблицы, для которых отсутствуют переменные xij), можно временно использовать
“запретные” клетки, задав для соответствующих временных переменных очень
большие удельные транспортные затраты (например, на порядок превышающие самые
большие значения параметров sij). Если исходная
задача разрешима, то в ходе реализации метода потенциалов несуществующие переменные
xij уйдут из числа
базисных. Если же все-таки окажется, что в оптимальный базис попала хотя бы
одна из запретных клеток, и значение соответствующей переменной положительно,
то это будет означать, что исходная задача была неразрешимой.
Еще один пример, приводящий к
нестандартной шахматной таблице – наличие среди ограничений 1. строгих
равенств, т.е. требования вывоза из некоторых пунктов всех наличных запасов
товара. Фактически этот пример сводится к предыдущему – отсутствие
дополнительной переменной, т.е. возможности поставки в фиктивный пункт
потребления из этих пунктов производства. В число запретных включаются соответствующие
клетки последнего столбца шахматной таблицы. Либо удается обойтись без них,
либо они временно “открываются” (но затраты на поставки в фиктивный пункт
потребления ставятся не нулевыми, а очень большими), и если все-таки окажется,
что какие-то из этих клеток остались в оптимальном решении, то это будет
означать, что задача разрешима, но в оптимальном решении в какие-то из пунктов
потребления будет поставлено товара больше минимально требуемого количества.
Для того, чтобы найти такое оптимальное решение (обычная шахматная таблица
позволяет находить оптимальное решение лишь для случая, когда суммарный объем
поставок в каждый пункт потребления в точности равен соответствующему значению b) требуется
переход к другой шахматной таблице, с большим количеством строк и столбцов.
Предлагаем читателям для тренировки самостоятельно построить шахматную таблицу,
соответствующую следующей постановке задачи: из пунктов производства необходимо
вывезти все наличные товары (все ограничения 1. заданы как строгие равенства),
суммарное их количество больше суммарного спроса (значения bj можно считать
минимально допустимыми суммарными объемами поставок в соответствующие пункты),
требуется обеспечить минимум суммарных транспортных затрат.
В заключение проведенного краткого экскурса в математические
транспортные задачи (ТЗ), приведем одну из возможных постановок экономической
проблемы, не имеющей отношения к перевозкам грузов, но которая сводится к
решению на основе типовой ТЗ.
Пример
1.1. Необходимо распределить работников по видам работ или же распределить отдельные
виды работ по работникам или по предприятиям, которые могут их выполнить. Пусть
ai –
суммарный за рассматриваемый период фонд рабочего времени i-го работника, sij – время,
требующееся работнику i для выполнения
единицы работы j (изделия вида
j); bj – суммарный объем работ j-го вида,
который необходимо выполнить (количество изделий вида j, которое необходимо
произвести). Требуется распределить фонд рабочего времени каждого работника по
выполняемым им видам работ так, чтобы минимизировать суммарное рабочее время,
требующееся для выполнения всех работ.
Математическая
постановка такой задачи полностью идентична стандартной транспортной задаче
типа 1. – 4. Также идентична ей будет и постановка задачи для решения проблемы
распределения по “подрядчикам” разных работ (bj – объем работ j-го вида, ai – суммарный
объем работ i-го вида,
который может выполнить i-й подрядчик, sij – плата за выполнение единицы работы вида j, которую берет подрядчик i) таким образом,
чтобы минимизировать суммарную стоимость выполнения всех работ.
ПРОСТЕЙШИЕ
ПРОИЗВОДСТВЕННО-ТРАНСПОРТНЫЕ МОДЕЛИ
Под простейшими транспортно-производственными моделями будем понимать
такие, которые по своему содержанию не являются задачами только по оптимизации
схем прикрепления потребителей к поставщикам, но которые из-за наличия особенностей
математической постановки могут быть сведены к математическим транспортным
задачам и не требуют для поиска оптимальных решений универсальных методов линейного
программирования.
В транспортных задачах часто
используется термин “пункт производства”, хотя собственно производство никаким
образом не рассматривается, так как в явном виде не учитываются
производственные затраты, а пункты вывоза продукции логичнее было бы называть
складами, на которых хранится уже произведенная продукция, и которую требуется
доставить потребителям с минимальными суммарными издержками на перевозки.
Перейдем теперь к моделям, в которых в
явном виде отражаются производственные затраты и в которых определяются не
только схемы прикрепления потребителей к поставщикам, но и производственные планы.
5.
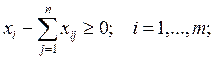
6.
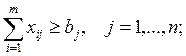
7.
![]()
8.
![]()
9.
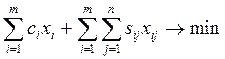
Здесь xi – искомый объем производства в пункте i;
ci – удельные производственные затраты в пункте
i;
ai – максимально возможный объем
выпуска продукции в пункте i. Смысл остальных переменных и
параметров остается таким же, как и в модели 1. – 4.
Если в ограничениях 7. изменить знаки на
противоположные, то полученная задача будет удовлетворять формальному
определению математической транспортной задачи: каждая переменная входит только
в два ограничения, причем в одно с коэффициентом “+1”, в другое с коэффициентом
“-1”. Но это будет задаче в сетевой постановке, которая также может быть решена
методом потенциалов, но процедура решения существенно более трудоемка при
ручном счете, неудобна такая постановка и для машинной реализации.
Возможно ли свести задачу 5. – 9. к
задаче шахматного типа? Очевидно (это легко доказать от противного), что при
положительных значениях всех параметров затрат ограничения 5. на оптимальном
плане всегда выполняются как равенства. Поэтому можно в них знак ≥
заменить на =, и при этом оптимальное решение не изменится. Далее ограничения
5. можно использовать для замены переменных
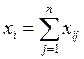
и подстановки в ограничения 7:
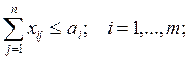
и в целевую функцию, которая примет вид:
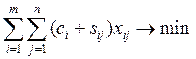 .
.
Полученная после таких простых
преобразований модель идентична задаче 1. – 4. с тем лишь отличием, что в коэффициентах
целевой функции стоят суммарные удельные производственные и транспортные затраты.
Таким образом, задачу 5. – 9. можно
сразу решать, используя стандартную шахматную таблицу, предварительно
рассчитав параметры ci +sij. Здесь также может потребоваться
фиктивный пункт потребления (затраты на поставку в него принимаются нулевыми),
если суммарные возможности производителей превышают суммарный спрос.
Небольшая дополнительная работа
потребуется, если возникнет необходимость найти решение двойственной к
5. – 9. задачи. Оценки ограничений 6. и 7. будут получены
непосредственно в шахматной таблице (после нормировки), ее потенциалы имеют
точно такой же смысл, как и оценки ограничений 6. и 7. Оценки ограничений 5.
легко посчитать позже, когда уже известны оценки ограничений 6. и 7. Для базисных
xi ограничения
двойственной к 5. – 9. задачи выглядят следующим образом: wi – ui = ci. где wi – искомые оценки ограничений 5., а ui – уже известные оценки ограничений 7. (эти
уравнения двойственной задачи записаны для случая, когда в прямой ограничения
7. приведены к виду ≥). Таким образом, оценки ограничений 5. отличаются
от соответствующих оценок ограничений 7. на величину удельных производственных
затрат, и при положительности параметров ci они всегда будут положительны. Оценки wi показывают, как изменится значение целевой функции
9. при увеличении соответствующей правой части ограничений 5. на единицу (экономически
это можно интерпретировать как требование поставки единицы продукции на склад
производителя).
Постановку задачи 5. - 9. можно
усложнить, вводя дополнительные ограничения, и во многих случаях новые задачи
будут сводимыми к математической транспортной задаче. Рассмотрим, как можно
учесть в шахматной таблице различные дополнительные ограничения.
1.
Требование
работы одного или нескольких предприятий на полную мощность.
Если бы изначально ограничения 5. были
заданы как строгие равенства, то такое требование было бы эквивалентно
требованию запрета поставок из соответствующих пунктов производства в фиктивный
пункт потребления. Так, если стоит условие xk = ak, то отсюда следует. что xkn+1 = 0 (или,
точнее, переменная xkn+1 при сведении
задачи к закрытой просто не появится). Как решать задачу. в которой некоторые
пункты производства не связаны с некоторыми пунктами потребления, уже известно
из предыдущего раздела. Проблема построения шахматной таблицы более сложной
структуры может возникнуть лишь в том случае, если суммарное предложение
предприятий, которые должны работать на полную мощность, превысит суммарный
спрос (в этом случае неизбежны «перепоставки» в
некоторые пункты потребления, возможность которых в в
обычной шахматной таблице не учитывается.
Теперь перейдем к рассмотрению
возможностей учета в задаче 5. – 9. других дополнительных условий,
причем, чтобы не рассматривать все многообразие возможных ситуаций, будем
предполагать, что эти ограничения будут достаточно слабыми, т.е. в оптимальном
плане не будет поставок в пункты потребления сверх заданных объемов спроса, а
производители не будут выпускать продукцию для собственных складов. Иначе
говоря, мы ограничимся пока возможностью учета дополнительных ограничений в
задаче следующего вида:
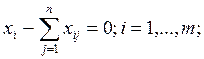
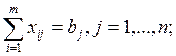
![]()
![]()
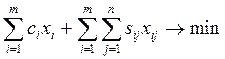
Аналогичные следующим ниже приемы учета
дополнительных ограничений в шахматных таблицах можно использовать и для
транспортно-производственной модели в исходной, более общей постановке (где
первые две группы ограничений заданы в виде неравенств), но тогда структура
получаемых шахматных таблиц будет немного сложнее, чем в рассматриваемых далее
упрощенных ситуациях.
2.
Наличие
ограничений снизу на объемы выпуска, т.е. ограничений следующего вида:
![]()
Эквивалентной заменой этих условий будут
следующие:
![]() , где
, где ![]() , а
, а ![]() .
.
Каждый пункт производства разбивается на два, первый из которых должен работать
на полную мощность, а допустимая вариация объема выпуска во втором находится в
интервале от нуля до величины разницы между максимально допустимым и минимально
допустимым значениями. В обоих пунктах одинаковы как производственные затраты,
так и затраты по доставке продукции во все пункты потребления.
Шахматная таблица, в которой учтены
ограничения снизу на объемы выпуска, будет иметь следующий вид:
|
b a |
b1 |
b2 |
… |
… |
… |
bn |
bn+1
|
|
a1 |
|
|
|
|
|
|
|
|
a1-a1 |
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
a2-a2 |
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
am |
|
|
|
|
|
|
|
|
am-am |
|
|
|
|
|
|
|
При наличии нижних положительных ограничений на объемы выпуска во всех
пунктах производства число строк в такой таблице будет в два раза больше, чем в
задаче, где нет ограничений снизу.
Обработка такой таблицы не представляет
проблем, и оптимальное решение исходной задачи получить нетрудно – для этого
необходимо выполнить обратную процедуру сложения значений полученных переменных:
![]() . Оценки всех
ограничений задачи (как основных, так и дополнительных) берутся непосредственно
из шахматной таблицы после нормировки ее потенциалов, либо рассчитываются путем
добавления к оценкам 3-й группы удельных производственных затрат (оценки 1-й
группы основных ограничений). Оценки ограничений снизу равны нулю, если
фактические значения объемов выпуска оказались выше заданных нижних границ,
либо положительны (тогда равны нулю оценки соответствующих основных ограничений,
т.е. ограничений сверху на объемы выпуска). В случае множественности оптимальных
решений возможно одновременное равенство нулю оценок и нижних, и верхних
ограничений на объемы выпуска.
. Оценки всех
ограничений задачи (как основных, так и дополнительных) берутся непосредственно
из шахматной таблицы после нормировки ее потенциалов, либо рассчитываются путем
добавления к оценкам 3-й группы удельных производственных затрат (оценки 1-й
группы основных ограничений). Оценки ограничений снизу равны нулю, если
фактические значения объемов выпуска оказались выше заданных нижних границ,
либо положительны (тогда равны нулю оценки соответствующих основных ограничений,
т.е. ограничений сверху на объемы выпуска). В случае множественности оптимальных
решений возможно одновременное равенство нулю оценок и нижних, и верхних
ограничений на объемы выпуска.
3.
Наличие
ограничений на суммарные объемы выпуска в двух или нескольких пунктах
производства. Это могут быть ограничения снизу, сверху или в виде равенства.
Пусть ограничение имеет вид: ![]() где
где ![]() (иначе оно будет эквивалентно требованию
работы на полную мощность всех предприятий, входящих в группу I*). Следствием из
него (или эквивалентным ограничением) является требование поставки из пунктов
производства
(иначе оно будет эквивалентно требованию
работы на полную мощность всех предприятий, входящих в группу I*). Следствием из
него (или эквивалентным ограничением) является требование поставки из пунктов
производства ![]() в фиктивный пункт производства продукции в
объеме
в фиктивный пункт производства продукции в
объеме ![]() , что
равнозначно
, что
равнозначно ![]() . Для учета
этого ограничения требуется разбить фиктивный пункт потребления на два, причем
поставки в первый из них допускаются только от предприятий группы I*, поставки во
второй допускаются только от предприятий, не входящих в группу I*. Суммарный
объем поставок в фиктивный пункт потребления от предприятий, не входящих в
группу I*, составит
. Для учета
этого ограничения требуется разбить фиктивный пункт потребления на два, причем
поставки в первый из них допускаются только от предприятий группы I*, поставки во
второй допускаются только от предприятий, не входящих в группу I*. Суммарный
объем поставок в фиктивный пункт потребления от предприятий, не входящих в
группу I*, составит ![]() . Структура шахматки, учитывающей данное
условие (n =
5; I*,={1; 4}) будет следующей:
. Структура шахматки, учитывающей данное
условие (n =
5; I*,={1; 4}) будет следующей:
|
b a |
b1 |
b2 |
b3 |
b4 |
b5 |
|
|
|
a1 |
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
|
Здесь в группу I* входят 1-й, 4-й
и 6-й пункты производства (![]() ) . После обработки этой таблицы и нахождения
оптимального решения можно найти и оценку ограничения
) . После обработки этой таблицы и нахождения
оптимального решения можно найти и оценку ограничения ![]() Увеличение A* на единицу
приводит к изменению в шахматной таблице двух параметров:
Увеличение A* на единицу
приводит к изменению в шахматной таблице двух параметров: ![]() и
и ![]() - первый из них уменьшается на единицу, второй
увеличивается. Потенциалы шахматной таблицы, в том числе последних двух
столбцов известны, поэтому оценка ограничения
- первый из них уменьшается на единицу, второй
увеличивается. Потенциалы шахматной таблицы, в том числе последних двух
столбцов известны, поэтому оценка ограничения ![]() может быть определена как
может быть определена как ![]() . Этот прием
нахождения оценок дополнительных ограничений рекомендуется и во многих других
случаях: определить, к каким изменениям a и b приведет изменение на малую величину правой части
того или иного дополнительного ограничения (при неизменности всех остальных),
умножить эти изменения на потенциалы соответствующих строк и столбцов и
результаты сложить.
. Этот прием
нахождения оценок дополнительных ограничений рекомендуется и во многих других
случаях: определить, к каким изменениям a и b приведет изменение на малую величину правой части
того или иного дополнительного ограничения (при неизменности всех остальных),
умножить эти изменения на потенциалы соответствующих строк и столбцов и
результаты сложить.
Ограничение на суммарные объемы выпуска
может быть задано и в виде неравенства, например, как ограничение снизу
(суммарный объем выпуска должен быть не менее заданной величины): ![]() . Соответствующая
такому ограничению структура шахматной таблицы будет следующей:
. Соответствующая
такому ограничению структура шахматной таблицы будет следующей:
|
b a |
b1 |
b2 |
b3 |
b4 |
b5 |
|
|
|
a1 |
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
|
Поставки в фиктивный пункт потребления
из входящих в группу I* пунктов производства
не превысят величины![]() , т.е. реальный
суммарный объем выпуска в них будет не меньше, чем A*.
, т.е. реальный
суммарный объем выпуска в них будет не меньше, чем A*.
Напротив, ограничение на суммарный объем
выпуска будет задано как ограничение сверху (![]() ), то
эквивалентным ограничением будет требование обеспечить суммарный объем
“поставок” в фиктивный пункт из пунктов производства, входящих в группу I* не менее, чем
), то
эквивалентным ограничением будет требование обеспечить суммарный объем
“поставок” в фиктивный пункт из пунктов производства, входящих в группу I* не менее, чем ![]() . Это требование
учитывается в шахматной таблице следующей структуры:
. Это требование
учитывается в шахматной таблице следующей структуры:
|
b a |
b1 |
b2 |
b3 |
b4 |
b5 |
|
|
|
a1 |
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
|
\\
Дополнительных суммарных ограничений
может быть и более одного, важно, чтобы они не были пересекающимися, т.е. чтобы
некоторые переменные не входили более чем в одно ограничение. В противном
случае сведение задачи с дополнительными ограничениями к «шахматке»
не всегда возможно.
4. Двусторонние ограничения на суммарный
объем выпуска: 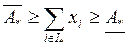 . Фактически это
не одно, а два ограничения, и их учет требует введения в шахматную таблицу еще
одного столбца. Необходимо, чтобы поставки в фиктивный пункт потребления от
поставщиков группы I* были не менее
чем
. Фактически это
не одно, а два ограничения, и их учет требует введения в шахматную таблицу еще
одного столбца. Необходимо, чтобы поставки в фиктивный пункт потребления от
поставщиков группы I* были не менее
чем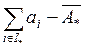 , но не более
чем
, но не более
чем ![]() . Для этого
фиктивный пункт потребления условно разбивается на три, в первый из которых
возможны лишь поставки из пунктов производства группы I* и объем
поставок должен быть равным
. Для этого
фиктивный пункт потребления условно разбивается на три, в первый из которых
возможны лишь поставки из пунктов производства группы I* и объем
поставок должен быть равным 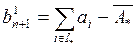 , во второй
возможны поставки из всех пунктов производства, и объем потребления в нем равен
, во второй
возможны поставки из всех пунктов производства, и объем потребления в нем равен
![]() , в третий же
поставки из пунктов производства группы I* запрещены (
, в третий же
поставки из пунктов производства группы I* запрещены (![]() ) .
) .
Шахматная таблица, в которой отражены
эти ограничения, будет иметь следующую структуру:
|
b a |
b1 |
b2 |
b3 |
b4 |
b5 |
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
|
a5 |
|
|
|
|
|
|
|
|
|
a6 |
|
|
|
|
|
|
|
|
Примеры:
В
исходной задаче 4 пункта производства и 3 пункта потребления. Соответствующие
объемы приведены в «шахматке».
Пусть
дополнительное ограничение задано в виде:
x1 + x4 < 60 .
Тогда
«шахматка» закрытой транспортной задачи будет
выглядеть следующим образом:
|
b a |
b1 30 |
b2 30 |
b3 30 |
Ф 40 |
ДФ 10 |
|
a1=20 |
|
|
|
|
|
|
a2=30 |
|
|
|
|
|
|
a3=40 |
|
|
|
|
|
|
a4=50 |
|
|
|
|
|
Объем
потребления в дополнительном фиктивном пункте равен
ДФ = a1 + a4 – 60= 20+50-60 = 10, а объем
потребления в «основном» фиктивном пункте корректируется на эту величину. Без
учета дополнительного ограничения разность 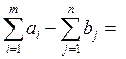 50, а теперь Ф =
40.
50, а теперь Ф =
40.
Если
бы дополнительное ограничение было бы задано в виде:
x1 + x4 > 60 ,
то
соответствующая «шахматка» закрытой транспортной
задачи выглядела бы следующим образом:
|
b a |
b1 30 |
b2 30 |
b3 30 |
Ф 40 |
ДФ 10 |
|
a1=20 |
|
|
|
|
|
|
a2=30 |
|
|
|
|
|
|
a3=40 |
|
|
|
|
|
|
a4=50 |
|
|
|
|
|
А
если бы дополнительное ограничение было бы задано в виде:
x1 + x4 = 60 ,
то
соответствующая «шахматка» закрытой транспортной
задачи выглядела бы следующим образом:
|
b a |
b1 30 |
b2 30 |
b3 30 |
Ф 40 |
ДФ 10 |
|
a1=20 |
|
|
|
|
|
|
a2=30 |
|
|
|
|
|
|
a3=40 |
|
|
|
|
|
|
a4=50 |
|
|
|
|
|
Двухстороннее
ограничение, типа:
60
< x1 + x4 < 65 .
потребовало
бы введение еще одного фиктивного пункта:
|
b a |
b1 30 |
b2 30 |
b3 30 |
Ф 40 |
ДФ1 5 |
ДФ2 5 |
|
a1=20 |
|
|
|
|
|
|
|
a2=30 |
|
|
|
|
|
|
|
a3=40 |
|
|
|
|
|
|
|
a4=50 |
|
|
|
|
|
|
Можно так прокомментировать введение
дополнительных фиктивных пунктов. Как минимум 5 единиц первый и четвертый пункты не
будут в сумме производить – обязательная поставка в первый дополнительный
фиктивный пункт (ДФ1), а
это означает выполнение условия
x1 + x4 < 65 ,
а
во второй фиктивный пункт (ДФ2)
поставки могут осуществляться из всех пунктов. То есть, если поставки сюда будут
только из первого и четвертого пункта, это будет означать «недопроизводство»
еще 5 единиц и
x1 + x4 = 60
При
поставках в этот пункт из других источников (второго и третьего):
x1 + x4 > 60
Дополнительные задания для
самостоятельного исследования.
1. Постройте шахматную таблицу,
позволяющую решить “задачу выбора потребителей” следующего вида:
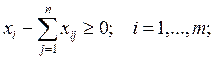
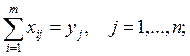
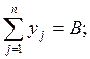
![]()
![]()
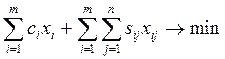
(объемы потребления в конкретных пунктах
– неизвестные величины, задан лишь суммарный объем потребления).
Можно ли решить эту задачу без
использования метода потенциалов и, тем более, универсальных алгоритмов? Если
да, то как?
2. Постройте шахматную таблицу для такой
же задачи, но в немного более сложной постановке – при наличии дополнительных
ограничений следующего вида: ![]()
3. Постройте шахматную таблицу для
“задачи размещения производителей” в следующей постановке:
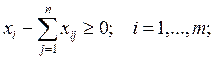
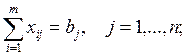
![]()
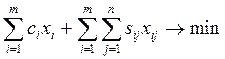
Здесь не ограничены возможности выпуска
во всех пунктах производства.
Можно ли решить эту задачу вообще без
построения шахматной таблицы, и если да, то каким образом.
МНОГОЭТАПНЫЕ
ПРОИЗВОДСТВЕННО-ТРАНСПОРТНЫЕ ЗАДАЧИ
Многоэтапными
производственно-транспортными задачами будем называть такие, которые отображают
последовательные процессы выпуска одного вида продукции, доставки его в пункты
переработки в другую продукцию, производства этой продукции и доставки ее
конечным потребителям. В самых простых постановках таких задач рассматриваются
два продукта – “сырье” и “готовый продукт”. Возможно и большее число
наименований: “сырье”, “полуфабрикат”, “готовый продукт”. При определенных
условиях и такие, формально многопродуктовые задачи, могут быть сведены к однопродуктовым задачам шахматного типа. Главное из этих
условий – одинаковые нормы расхода одной продукции на производство другой во
всех пунктах переработки.
Формальная
постановка самой простой многоэтапной задачи:
10.
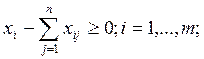
11.
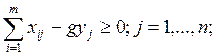
12.
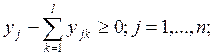
13.
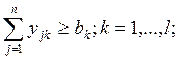
14.
![]()
15.
![]()
16.
![]()
17.
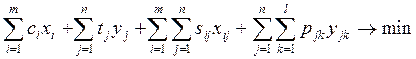
Обозначения: xi – искомый объем добычи сырья в пункте i;
yj – искомый объем производства
готовой продукции в пункте j; xij – искомый объем
перевозок сырья из пункта i в пункт j; yjk – искомый объем
перевозки готовой продукции из пункта j в пункт k; ai – максимально возможный объем добычи
сырья в пункте i; qj – максимально
возможный объем выпуска готовой продукции в пункте j; g – расход сырья на единицу готовой продукции; ci – удельные
затраты на добычу сырья в пункте i; tj - удельные затраты на
производство готовой продукции в пункте j; sij - удельные затраты на перевозку сырья из пункта
i в пункт
j;
pjk – удельные
затраты на перевозку готовой продукции из пункта j в пункт k; bk – спрос на готовую продукцию в
пункте k.
Целевой функцией является минимизация
всех суммарных затрат на производство и транспортировку сырья и готовой
продукции.
Модель
10. – 17. нельзя свести к математической транспортной задаче лишь путем
изменения знаков в ограничениях 14. и 15.
Во-первых,
среди коэффициентов матрицы A есть не только нули и единицы,
во-вторых, некоторые переменные (yj) встречаются в ограничениях не
два, а три раза.
Первую проблему легко решить путем
замены переменных: gyj = ![]() . Экономически это соответствует переходу к новой
единице измерения готовой продукции – количеству сырья, пошедшему на ее
изготовление (аналогичный прием используется иногда и в реальности, например,
объем производства цельномолочной продукции в промышленности – молока разных
видов, сливок, сметаны, кефира и т.п. – измеряется количеством молока
определенной жирности, пошедшего на изготовление разнообразных молочных
продуктов).
. Экономически это соответствует переходу к новой
единице измерения готовой продукции – количеству сырья, пошедшему на ее
изготовление (аналогичный прием используется иногда и в реальности, например,
объем производства цельномолочной продукции в промышленности – молока разных
видов, сливок, сметаны, кефира и т.п. – измеряется количеством молока
определенной жирности, пошедшего на изготовление разнообразных молочных
продуктов).
После
замены переменных в ограничениях 11. уже нет коэффициентов, отличных от нуля и
единицы. Далее аналогичный переход к новым единицам измерения осуществляется в
ограничениях 12., 13. и 15. – их правые и левые части умножаются на g, после чего
вместо прежних переменных и параметров вводятся новые: gyjk = ![]() ; gbk =
; gbk = ![]() ; gqj =
; gqj = ![]() . В целевой функции в связи с заменой переменных также
происходит замена параметров:
. В целевой функции в связи с заменой переменных также
происходит замена параметров: ![]() .
.![]()
После
замены переменных и параметров модель 10. – 17. будет иметь следующий вид:
10а.
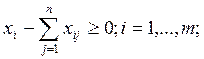
11а.
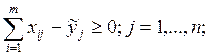
12а.
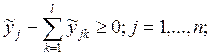
13а.
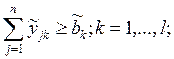
14а.
![]()
15а.
![]()
16а.
![]()
17а.
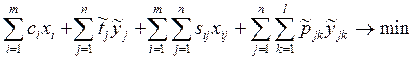
В
полученной задаче остается один “дефект” – переменные ![]() встречаются не в
двух, а в трех ограничениях. Его легко устранить, если доказать, что
ограничения 11а. на оптимальном плане выполняются как равенства (это легко
сделать от противного), использовать эти равенства для выражения
встречаются не в
двух, а в трех ограничениях. Его легко устранить, если доказать, что
ограничения 11а. на оптимальном плане выполняются как равенства (это легко
сделать от противного), использовать эти равенства для выражения ![]() через суммы xij, и осуществить подстановку в
ограничения 12а. В ограничениях 14а. и 15а. изменим знаки на противоположные и
получим задачу, удовлетворяющую определению математической транспортной задачи.
Но это будет задача в сетевой постановке, и для перехода к задаче шахматного
типа необходимо будет избавиться от переменных xi
и
через суммы xij, и осуществить подстановку в
ограничения 12а. В ограничениях 14а. и 15а. изменим знаки на противоположные и
получим задачу, удовлетворяющую определению математической транспортной задачи.
Но это будет задача в сетевой постановке, и для перехода к задаче шахматного
типа необходимо будет избавиться от переменных xi
и ![]() .
.
Легко
доказать от противного, что при положительных параметрах затрат ограничения
10а., 11а., 12а, 13а. на оптимальном плане выполняются как равенства. Первые
три из них можно использовать для замены переменных и подстановки в другие
ограничения. Выразим xi через суммы объемов вывоза и эти
выражения подставим в ограничения 14а. Выразим ![]() через суммы объемов ввоза и подставим в ограничения
15а. Одновременно справедливым должно быть ограничение, полученное путем подстановки
в 15а. выражений
через суммы объемов ввоза и подставим в ограничения
15а. Одновременно справедливым должно быть ограничение, полученное путем подстановки
в 15а. выражений ![]() через суммы объемов вывоза, полученных из 12а. В результате
всех подстановок получим следующую совокупность ограничений:
через суммы объемов вывоза, полученных из 12а. В результате
всех подстановок получим следующую совокупность ограничений:
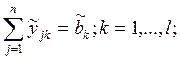
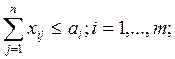
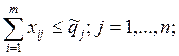
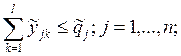
Сводим
последние три группы ограничений к равенствам путем введения дополнительных
переменных, причем в последние две группы неравенств не потребуются разные
дополнительные переменные, поскольку правые части у них совпадают, и нам
известно также, что 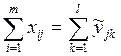 . Обозначим эти переменные как zjj , получим следующую систему равенств:
. Обозначим эти переменные как zjj , получим следующую систему равенств:
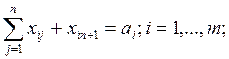
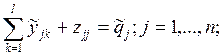
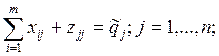
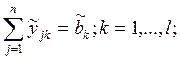
Для удобства ограничения переставлены местами. Первые две группы
ограничений являются строчными (изменяется второй индекс, распределяется по
потребителям произведенная продукция), вторые две группы – столбцовыми
(изменяется первый индекс, складываются объемы поставок от разных производителей).
В этой задаче две группы производителей – производители сырья и производители
готовой продукции, а также две группы потребителей – потребители сырья и
потребители готовой продукции. Достаточное и необходимое условие разрешимости
такой задачи – выполнение одновременно двух условий:
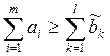 и
и 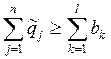 .
.
После подстановок использованных выражений переменных в целевую функцию
она приобретет следующий вид:
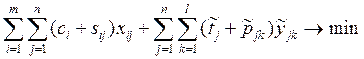
При всех
дополнительных переменных коэффициенты нулевые.
Структура
шахматной таблицы, соответствующей последней группе равенств, будет следующей (m=n=l=3):
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
0 |
|
a2 |
|
|
|
|
|
|
0 |
|
a3 |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Здесь 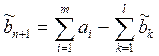 .
.
После подготовки информации (пересчета параметров) решение задачи на
ЭВМ осуществляется точно так же, как и для простых однопродуктовых
задач – в клетки, переменных для которых не существует, в качестве
коэффициентов целевой функции ставятся большие числа, и если исходная задача
разрешима, в оптимальном плане значения переменных в этих клетках будут
нулевыми. При ручном счете и буквальном использовании метода северо-западного
угла для построения первоначального плана может возникнуть необходимость
временного использования запретных клеток. Чтобы этого избежать, рекомендуется вначале заполнить последний столбец
шахматной таблицы – сверху или снизу ставя в его клетки максимально
возможные числа. Другой прием – переставить столбцы – поставить последний
впереди всех остальных (в этом случае пригоден будет и обычный метод построения
– сначала удовлетворяются потребности первого пункта потребления, затем второго
и т.д.
После построения первоначального плана дальнейшая обработка шахматной таблицы
осуществляется так же как и для простых транспортных задач, с тем лишь
отличием, что получаемые здесь цепочки из “+” и “-“ могут быть достаточно длинными.
Пример построения первоначальной шахматной таблицы.
Пусть параметры многоэтапной производственно-транспортной задачи
таковы:
a = (50, 70, 90); q = (30, 80, 60); b = (40, 30, 50);
c = (5, 6, 4); t = (3, 6, 9);
|
|
3 |
4 |
6 |
|
|
9 |
18 |
6 |
|
|
|
|
{s}
= |
2 |
5 |
1 |
|
{p}
= |
6 |
12 |
15 |
|
g
= 1,5 |
|
|
|
8 |
3 |
4 |
|
|
3 |
15 |
21 |
|
|
|
После перехода к
новым единицам измерения получаем:
![]() = (45, 120, 90);
= (45, 120, 90); ![]() = (60, 45, 75);
= (60, 45, 75); ![]() =
(2, 4, 6);
=
(2, 4, 6);
|
|
6 |
12 |
4 |
|
{ |
4 |
9 |
10 |
|
|
2 |
10 |
14 |
Находим также ![]() = 30.
= 30.
Шахматная таблица с
первоначальным планом имеет следующий вид:
|
|
45 |
120 |
90 |
60 |
45 |
75 |
30 |
ui |
|
50 |
8 45 |
9 5 |
11 |
|
|
|
0 |
0 |
|
70 |
8 |
11 70 |
7 |
|
|
|
0 |
-2 |
|
90 |
12 |
7 45 |
8 15 |
|
|
|
0 30 |
2 |
|
45 |
0 |
|
|
8 45 |
14 |
6 |
|
16 |
|
120 |
|
0 |
|
8 15 |
13 45 |
14 60 |
|
16 |
|
90 |
|
|
0 75 |
8 |
16 |
20 15 |
|
10 |
|
vj |
8 |
9 |
10 |
24 |
29 |
30 |
2 |
|
Возможны и другие варианты
первоначального плана. В нашем случае последовательность заполнения клеток была
следующей (при сплошной нумерации их координат): (3,7) = 30 → (1,1) = 45
→ (1,2) = 5 → (2,2) = 70 → (2,3) = 15 → (6,3) = 75
→ (4,4) = 45 → (5,4) = 15 → (5,5) = 45 → (5,6) = 60
→ (6,6) = 15.
Расчет переменных двойственной задачи
практически не отличается от той схемы, которая использовалась в самом первом
примере. В качестве начальной была выбрана с нулевым значением оценка первого
пункта заготовки сырья. Полученная система оценок не нормировалась, в этом нет
необходимости, так как первоначальный план не является оптимальным.
Не будем показывать здесь всю
последовательность итераций по пересчету шахматной таблицы, приведем лишь
заключительный, оптимальный план.
|
|
45 |
120 |
90 |
60 |
45 |
75 |
30 |
ui |
|
50 |
8 45 |
9 |
11 |
|
|
|
0 5 |
0 |
|
70 |
8 |
11 |
7 60 |
|
|
|
0 10 |
0 |
|
90 |
12 |
7 75 |
8 |
|
|
|
0 15 |
0 |
|
45 |
0 |
|
|
8 |
14 |
6 45 |
|
15 |
|
120 |
|
0 45 |
|
8 |
13 45 |
14 30 |
|
7 |
|
90 |
|
|
0 30 |
8 60 |
16 |
20 15 |
|
7 |
|
vj |
8 |
7 |
7 |
15 |
20 |
21 |
0 |
|
Потенциалы шахматной таблицы сразу
позволяют найти некоторые оценки задачи 10а. – 17а. Это оценки ограничений 13а.
(15, 20, 21) и ограничений 14а. (0, 0, 0). Для нахождения остальных необходимо
посмотреть, какие изменения произойдут в шахматной таблице при увеличении их
правых частей на 1. Легко находятся оценки ограничений 15а.: (8-15, 7-7, 7-7) =
(-7, 0, 0). Увеличение значения ![]() на единицу приводит
к изменению сразу двух чисел – и объема производства, и объема потребления в
соответствующем пункте.
на единицу приводит
к изменению сразу двух чисел – и объема производства, и объема потребления в
соответствующем пункте.
Что произойдет в шахматной таблице при
увеличении на 1 правой части какого-либо ограничения из 10а.? Фактически это
означает требование поставки единицы продукции на склад производителя, т.е. в шахматной
таблице появится еще один потребитель (еще один столбец), к которому ведет лишь
один маршрут (в столбце свободна лишь одна клетка и она всегда будет входить в
число базисных). Оценка пункта производства известна, для вычисления оценки
пункта потребления необходимо прибавить к ней транспортные затраты (сумму
производственных и транспортных затрат, а поскольку транспортные затраты по
поставке на собственный склад равны 0, то в качестве коэффициента целевой
функции в этой дополнительной клетке шахматной таблицы будут только
производственные затраты). Таким образом, для вычисления оценок ограничений
10а. необходимо к потенциалам первых трех строк шахматной таблицы добавить
производственные затраты: (0+5, 0+6, 0+4) = (5, 6, 4).
Эти же оценки можно получить и иным
путем. Все переменные xi
входят в оптимальный базис, можно выписать для них уравнения
двойственной задачи, из которых будет очевидно, что оценки ограничений 10а. и
14а. отличаются на величину удельных производственных затрат.
Аналогичными приемами – через изменение
шахматной таблицы или напрямую через уравнения двойственной задачи – можно
вычислить оценки всех остальных ограничений задачи 10а. – 17а. Помните только,
что как равенства ограничения двойственной задачи выполняются только для
базисных переменных.
Получив оценки всех ограничений задачи
10а. – 17а., нетрудно вычислить и оценки ограничений исходной задачи 10. – 17.
Они будут отличаться от полученных только для тех ограничений, где был
осуществлен переход к новым единицам измерения. Увеличение на 1 правой части
ограничений 12а., 13а. и 15а. эквивалентно в нашем примере увеличению на 2/3
соответствующих правых частей в ограничениях 12., 13. и 15. Поэтому все оценки
этих трех групп ограничений будут в полтора раза больше полученных для ограничений
12а., 13а. и 15а.
Многоэтапные задачи позволяют, не выходя
за рамки шахматных таблиц (т.е. без необходимости прибегать к универсальным
методам решения задач линейного программирования), учитывать большее число
дополнительных ограничений, чем в простейших производственно-транспортных
задачах. В частности, все дополнительные ограничения в части работы пунктов по
добыче сырья учитываются точно так же, как это делалось в предыдущем разделе –
через переход к эквивалентным ограничениям на поставки в фиктивный пункт
потребления (условия работы на полную мощность, нижние границы на объемы
выпуска, односторонние и двусторонние суммарные ограничения). Для пунктов
переработки легко учесть в шахматной таблице только условия работы на полную
мощность и ограничения снизу на объемы выпуска (запрет поставок через
диагональные клетки, для которых отсутствуют переменные zjj, условная разбивка пункта переработки
на два, один из которых должен работать на полную мощность). Суммарные
ограничения на объемы выпуска перерабатывающих предприятий путем изменения
структуры шахматной таблицы учесть невозможно.
Среди других дополнительных ограничений
можно назвать такие как условия резервирования (увеличения запасов и затраты на
хранение):
а) сырья на складах заготовительных предприятий;
б) сырья на складах перерабатывающих
предприятий;
в) готовой продукции на складах
перерабатывающих предприятий.
Эти склады можно интерпретировать как
дополнительные пункты потребления с известными затратами на производство и
транспортировку продукции туда от поставщиков, поэтому учет всех таких ограничений
достигается за счет введения в шахматную таблицу дополнительных столбцов.
Методы расчета оценок дополнительных
ограничений – либо через потенциалы шахматной таблицы и учет изменений ее
параметров при изменении на единицу правых частей этих ограничений, либо
напрямую – через уже известные оценки ограничений и уравнения двойственной
задачи для переменных, вошедших в оптимальный базис.
В заключение остается добавить, что
иногда с целью избежать появления дробных значений удобнее сделать замену не
переменных y
и параметров q
и b,
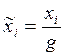
а переменных x и параметров a. (
и т.д.). На структуру шахматной таблицы это никак не влияет, изменятся
лишь числа, стоящие в клетках таблицы.
ТРАНСПОРТНЫЕ И
ТРАНСПОРТНО–ПРОИЗВОДСТВЕННЫЕ ЗАДАЧИ, ВКЛЮЧАЮЩИЕ ОГРАНИЧЕНИЕ ОБЩЕГО ВИДА
Пусть требуется решить стандартную ТЗ с
дополнительным ограничением типа
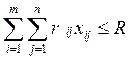 (ресурсное ограничение).
(ресурсное ограничение).
![]() - расход ограниченного ресурса на транспортировку
единицы продукции из пункта i в пункт j,
- расход ограниченного ресурса на транспортировку
единицы продукции из пункта i в пункт j,
![]() -
общее количество ресурса, выделенного системе.
-
общее количество ресурса, выделенного системе.
Решаем задачу без дополнительного
ограничения. Получив оптимальный план, считаем
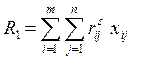
Если ![]() то
дополнительное ограничение несущественно, если
то
дополнительное ограничение несущественно, если ![]() ищем направление
изменения плана, по которому экономия каждой единицы ресурса достигается с
минимальным приростом затрат.
ищем направление
изменения плана, по которому экономия каждой единицы ресурса достигается с
минимальным приростом затрат.
Шаг 1. Решаем систему уравнений![]() для базисных
для базисных ![]() .
.
Шаг 2. Включение в базис
переменных, для которых ![]() что приводит к
уменьшению расхода ресурса.
что приводит к
уменьшению расхода ресурса.
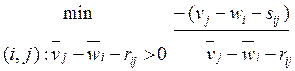 Шаг 3.
Рассчитываем
Шаг 3.
Рассчитываем
![]() =
=
Шаг 4. Переменную ![]() , для которой достигается минимум, включаем в базис
(процедура изменения базиса такая же, как при решении ТЗ методом потенциалов),
при этом экономия ресурса составит:
, для которой достигается минимум, включаем в базис
(процедура изменения базиса такая же, как при решении ТЗ методом потенциалов),
при этом экономия ресурса составит:
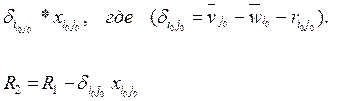 .
.
![]()
Если то получен оптимальный план.
![]()
Если то необходимо «вернуться
назад» и включить новую переменную в базис
с интенсивностью (величиной, которая перераспределяется по контуру),
равной ![]() .
.
![]() Если то продолжаем процесс, т.е. для
нового опорного плана рассчитываем
Если то продолжаем процесс, т.е. для
нового опорного плана рассчитываем
![]()
находим минимальное отношение прироста затрат на
единицу экономии ресурса, включаем соответствующую переменную в базис и т.д.
Пример.
Пусть a
= (10, 20, 30), b
= (15, 22, 23); R=270
|
|
4 |
6 |
9 |
|
|
6 |
5 |
2 |
|
sij= |
5 |
3 |
6 |
|
rij= |
5 |
7 |
5 |
|
|
6 |
9 |
7 |
|
|
4 |
1 |
2 |
Решается задача без учета ресурсного
ограничения: находим решение, двойственные оценки и стоимостные невязки.
Оптимальный план Оценки Невязки
|
|
15 |
22 |
23 |
|
|
||
|
10 |
4 |
6 |
9 |
2 |
|
|
-4 |
|
8 |
2 |
|
|||||
|
20 |
5 |
3 |
6 |
5 |
-4 |
|
-4 |
|
|
20 |
|
|||||
|
30 |
6 |
9 |
7 |
0 |
|
-1 |
|
|
7 |
|
23 |
|||||
|
vj |
6 |
8 |
7 |
|
|
|
|
Целевая функция (минимум затрат)
8*4+2*6+20*3+7*6+23*7=307, а расход дефицитного ресурса в оптимальном плане: R1=272
> R=270 !!
Посчитаем оценки и невязки для базиса
оптимального плана (затемненные клетки) по матрице коэффициентов дефицитного
ресурса.
|
«Ресурсные»
оценки, по оптимальному базису |
|
«Невязки»
по ресурсам |
||||||||||
|
|
|
для xi j= 0 |
||||||||||
|
|
6 |
5 |
2 |
0 |
|
|
2 |
|||||
|
|
5 |
7 |
5 |
-2 |
3 |
|
1 |
|||||
|
|
4 |
1 |
2 |
2 |
|
2 |
|
|||||
|
|
6 |
5 |
4 |
|
|
|
|
|||||
Все
небазисные невязки больше 0. Это значит, если в любой из этих клеток появится
поставка, то это приведет к уменьшению расхода дефицитного ресурса.
Чтобы
выбрать лучшую клетку, куда перераспределятся поставки, необходимо рассчитать
матрицу отношений стоимостных и ресурсных невязок, то есть значения:
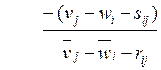
Эти
величины показывают удельный прирост затрат на единицу экономии ресурса, и
среди них надо выбрать минимальное
|
|
|
2 |
Минимум
реализуется на клетке (3;2), переменную x32
вводим в базис |
(+) 8 |
(-) 2 |
|
|
1.333 |
|
4 |
|
20 |
|
|
|
|
0.5 |
|
(-) 7 |
( + ) |
23 |
Строим цепочку, по которой будет
осуществляться перераспределение. Цепочка из "+" и "-"
строится однозначно и только по базисным клеткам. По цепочке двигаем
минимальное из отрицательных объемов (-2 и -7)=-2. При этом экономия ресурса будет
равна произведению (δ32=2) * (объем перераспределяемый по
цепочке = 2) = 4.
Промежуточный план
|
|
15 |
22 |
23 |
|
10 |
4 |
6 |
9 |
|
10 |
|
|
|
|
20 |
5 |
3 |
6 |
|
|
20 |
|
|
|
30 |
6 |
9 |
7 |
|
5 |
2 |
23 |
План по затратам ухудшился
10*4+20*3+5*6+2*9+23*7=309
Расход дефицитного ресурса в новом
плане: R2=268 < R=270 мы «переэкономили» ресурс.
Но это значит что мы понесли
дополнительные затраты, так как каждая единица перераспределяемая по «контуру»
увеличивает затраты на величину соответствующей невязки. Чтобы этого избежать
на этой итерации можно построить такой план, который использует весь объем
ресурса при минимально возможной величине затрат. Для этого надо
ориентироваться на величину (R1-R) = 2 в нашем случае и по «контуру» перераспределять
величину равную (R1-R)/ δ32=( 272-270)/2=1
При этом транспортные затраты по
отношению к исходному оптимальному плану вырастут на величину невязки
умноженной на величину перераспределения по контуру, т.е. 307+1*1=308, а расход
ресурса будет равен заданной величине 270.
Отметим, что оценка ограничения по дефицитному ресурсу равна![]() =2.
=2.
Конечный
вариант плана
|
|
15 |
22 |
23 |
|
10 |
4 |
6 |
9 |
|
9 |
1 |
|
|
|
20 |
5 |
3 |
6 |
|
|
20 |
|
|
|
30 |
6 |
9 |
7 |
|
6 |
1 |
23 |
Если бы заданный объем был равен,
например 265, то нам пришлось бы делать дополнительные итерации.
Во-первых, на первой итерации
максимально сэкономили ресурс, т.е. по контуру перемещали максимально возможный
объем равный 2.
Во-вторых надо скорректировать матрицу
транспортных затрат с учетом оценки дефицитного ресурса![]() полученной на этой итерации:
полученной на этой итерации:
![]()
В этих скорректированных затратах
полученный новый вариант плана будет оптимальным.
А далее повторяем Шаг 1 – Шаг 4
алгоритма, пока не выйдем на заданный объем дефицитного ресурса.
Постановка
и методы решения производственных и
производственно-транспортных моделей
Динамическое программирование.
Термин «динамическое программирование»
не столько определяет особый тип задач, сколько характеризует методы нахождения
решения отдельных классов задач математического программирования, которые могут
относиться к задачам как линейного, так и не линейного программирования. Рассматривается достаточно широкий класс задач на
определение оптимальной стратегии к которым относятся: функционирование
промышленного предприятия в течении определенного времени, транспортная задача,
прокладка наивыгоднейшего пути (железной дороги, автострады и т.п.) между двумя
пунктами с учетом особенностей местности, некоторые задачи целочисленного
программирования и т.д.
Динамическое программирование – один из
разделов оптимального программирования, в котором процесс принятия решения и
управления может быть разбит на отдельные этапы (шаги).
Например, при распределении на несколько
лет ресурсов, предназначенных для деятельности предприятия, шагом целесообразно
считать временной период; при распределении средств между предприятиями – номер
очередного предприятия. В других задачах разбиение на шаги вводится
искусственно. Например, непрерывный управляемый процесс можно рассматривать как
дискретный, условно разбив его на временные отрезки (шаги). Исходя из условий
каждой конкретной задачи, длину шага выбирают таким образом, чтобы на каждом
шаге получить простую задачу оптимизации и обеспечить требуемую точность
вычислений.
Иными словами, нахождение решения конкретных
задач методами динамического программирования включает несколько шагов, на
каждом из которых определяется решение некоторой частной задачи, обусловленной
исходной. Поэтому термин «динамическое программирование» не столько определяет
особый тип задач, сколько характеризует методы нахождения решения отдельных
классов задач математического программирования, которые могут относиться к
задачам как линейного, так и нелинейного программирования. Попытаемся
сформулировать общую постановку задачи динамического программирования и
определить единый подход к ее решению.
Предположим, что данная экономическая
система S находится в некотором начальном состоянии ![]() и является
управляемой. Таким образом, благодаря осуществлению некоторого управления U указанная система переходит из начального состояния
и является
управляемой. Таким образом, благодаря осуществлению некоторого управления U указанная система переходит из начального состояния
![]() в конечное состояние
в конечное состояние ![]() . При этом качество каждого из реализуемых
управлений U
характеризуется соответствующим значением функции W(U). Задача состоит в том, чтобы из
множества возможных управлений U найти такое
. При этом качество каждого из реализуемых
управлений U
характеризуется соответствующим значением функции W(U). Задача состоит в том, чтобы из
множества возможных управлений U найти такое ![]() , при котором функция W(U) принимает экстремальное (максимальное
или минимальное) значение
, при котором функция W(U) принимает экстремальное (максимальное
или минимальное) значение ![]() . Сформулированная задача и является общей задачей
динамического программирования.
. Сформулированная задача и является общей задачей
динамического программирования.
Дадим геометрическую интерпретацию этой
задачи. Предположим, что состояние системы характеризуется некоторой точкой S на плоскости X10X2 (рис1) и эта точка благодаря осуществляемому управлению ее
движением перемещается вдоль линии, изображенной на рис. 1, из области
возможных начальных состояний ![]() в область
допустимых конечных состояний
в область
допустимых конечных состояний ![]() .
.
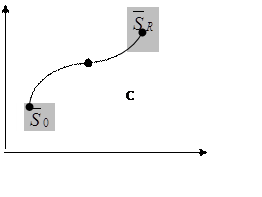
Рисунок
1. Иллюстрация метода динамического программирования.
Каждому управлению U движением точки, т.е. каждой траектории движения
точки, поставим в соответствие значение некоторой функции W(U) (например, длину
пути, пройденного точкой под воздействием данного управления. Тогда задача состоит
в том, чтобы из всех допустимых траекторий движения точки S найти такую,
которая получается в результате реализации управления ![]() , обеспечивающего экстремальное значение функции
, обеспечивающего экстремальное значение функции ![]() . К определению такой «траектории» сводится и задача
динамического программирования в случае, когда допустимые состояния системы S определяются точками n
– мерного пространства.
. К определению такой «траектории» сводится и задача
динамического программирования в случае, когда допустимые состояния системы S определяются точками n
– мерного пространства.
Отметим важное свойство оптимальной
траектории: если точка С находится на оптимальной
траектории движения, то оптимальный переход (траектория движения) из этой точки
в область допустимых конечных состояний ![]() совпадает с
общей оптимальной траекторией.
совпадает с
общей оптимальной траекторией.
Экономическую интерпретацию общей задачи
динамического программирования рассмотрим на конкретном примере.
1. Для увеличения объемов выпуска
пользующейся повышенным спросом продукции, изготовляемой предприятиями,
выделены капитальные вложения в объеме S
тыс. руб.
Использование i-м предприятием xi тыс. руб. из
указанных средств обеспечивает прирост выпуска продукции, определяемый
значением нелинейной функции ![]() .
.
Найти распределение капитальных вложений
между предприятиями, обеспечивающее максимальное увеличение выпуска продукции.
Математическая постановка задачи состоит
в определении наибольшего значения функции
(1) 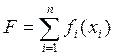
При условиях:
(2) 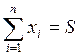
(3) ![]()
Сформулированная задача является задачей
нелинейного программирования. В том случае, когда ![]() - выпуклые (или
вогнутые) функции, ее решение можно найти, например, методом множителей
Лагранжа. Если же функции
- выпуклые (или
вогнутые) функции, ее решение можно найти, например, методом множителей
Лагранжа. Если же функции ![]() не являются
таковыми, то известные методы нахождения решения задач нелинейного программирования
не позволяют определить глобальный максимум функции (1). Тогда решение задачи
(1) – (3) можно найти с помощью динамического программирования. Для этого
исходную задачу нужно рассмотреть как многошаговую. Вместо того чтобы
рассматривать допустимые варианты распределения капиталовложений между n предприятиями и
оценивать их эффективность, будем исследовать эффективность вложения средств на
одном предприятии, на двух предприятиях и т. д., наконец на n предприятиях.
Таким образом, получим n этапов, на каждом из которых состояние системы (в
качестве которой выступают предприятия) описывается объемом средств, подлежащих
освоению k
предприятиями
не являются
таковыми, то известные методы нахождения решения задач нелинейного программирования
не позволяют определить глобальный максимум функции (1). Тогда решение задачи
(1) – (3) можно найти с помощью динамического программирования. Для этого
исходную задачу нужно рассмотреть как многошаговую. Вместо того чтобы
рассматривать допустимые варианты распределения капиталовложений между n предприятиями и
оценивать их эффективность, будем исследовать эффективность вложения средств на
одном предприятии, на двух предприятиях и т. д., наконец на n предприятиях.
Таким образом, получим n этапов, на каждом из которых состояние системы (в
качестве которой выступают предприятия) описывается объемом средств, подлежащих
освоению k
предприятиями ![]() . Решение об объемах капиталовложений, выделяемых k-му предприятию
. Решение об объемах капиталовложений, выделяемых k-му предприятию ![]() , и являются управлениями. Задача состоит в выборе
таких управлений, при которых функция (1) принимает наибольшее значение.
, и являются управлениями. Задача состоит в выборе
таких управлений, при которых функция (1) принимает наибольшее значение.
Нахождение решения
задач методом динамического программирования.
Рассмотрим в общем виде решение задачи
динамического программирования.
Будем считать, что состояние
рассматриваемой системы S на k-ом шаге ![]() определяется совокупностью
чисел
определяется совокупностью
чисел ![]() которые получены
в результате реализации управления
которые получены
в результате реализации управления ![]() , обеспечивающего переход системы S из состояния
, обеспечивающего переход системы S из состояния ![]() в состояние
в состояние ![]() . При этом будем предполагать, что состояние
. При этом будем предполагать, что состояние ![]() в которое пришла
система S, зависит от данного состояния
в которое пришла
система S, зависит от данного состояния ![]() и выбранного
управления
и выбранного
управления ![]() и не зависит от
того, каким образом система S пришла в
состояние
и не зависит от
того, каким образом система S пришла в
состояние ![]() .
.
Далее, будем считать, что если в
результате реализации k- го шага
обеспечен определенный доход или выигрыш, также зависящий от исходного
состояния системы ![]() и выбранного
управления
и выбранного
управления ![]() и равный
и равный ![]() , то общий доход или выигрыш за n шагов составляет
, то общий доход или выигрыш за n шагов составляет
(4) 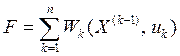 .
.
Таким образом, мы сформулировали два
условия, которым должна удовлетворять рассматриваемая задача динамического
программирования. Первое условие обычно называют условием отсутствия последствия, а второе – аддитивности целевой функции задачи.
Выполнение для задачи динамического
программирования первого условия позволяет сформулировать для нее принцип
оптимальности Беллмана. Прежде чем сделать это, дадим определение оптимальной стратегии управления. Под
такой стратегией будем понимать совокупность управлений ![]() , в результате реализации которых система S за n шагов переходит
из начального состояния
, в результате реализации которых система S за n шагов переходит
из начального состояния ![]() в конечное
в конечное ![]() и при этом функция
(4) принимает наибольшее значение.
и при этом функция
(4) принимает наибольшее значение.
Принцип
оптимальности. Каково бы ни было состояние системы перед
очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном
шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.
Отсюда следует, что оптимальную
стратегию управления можно получить, если сначала найти оптимальную стратегию
управления на m –м шаге, затем на двух последних шагах, затем на
трех последних шагах и т.д., вплоть до первого шага. Таким образом, решение рассматриваемой
задачи динамического программирования целесообразно начинать с определения
оптимального решения на последнем, m – м шаге. Для того чтобы найти это решение,
очевидно, нужно сделать различные предположения о том, как мог окончиться
предпоследний шаг, и с учетом этого выбрать управление ![]() , обеспечивающее максимальное значение функции
, обеспечивающее максимальное значение функции ![]() . Такое управление
. Такое управление ![]() , выбранное при определенных предположениях о том, как
окончился предыдущий шаг, называется условно
оптимальным управлением. Следовательно, принцип оптимальности требует
находить на каждом шаге условно оптимальное управление для любого из возможных
исходов предыдущего шага.
, выбранное при определенных предположениях о том, как
окончился предыдущий шаг, называется условно
оптимальным управлением. Следовательно, принцип оптимальности требует
находить на каждом шаге условно оптимальное управление для любого из возможных
исходов предыдущего шага.
В отличие от линейного программирования,
в котором симплекс метод является универсальным методом решения, в динамическом
программировании такого универсального метода не существует. Одним из основных
методов динамического программирования является метод рекуррентных соотношений,
который основывается на использовании принципа оптимальности, разработанного
американским математиком Р. Беллманом. Принцип состоит в том, что, каковы бы ни
были начальное состояние на любом шаге и управление, выбранное на этом шаге,
последующие управления должны выбираться оптимальными относительно состояния, к
которому придет система в конце данного шага. Использование данного принципа
гарантирует, что управление, выбранное на любом шаге, не локально лучше, а
лучше с точки зрения процесса в целом.
Суть метода динамического
программирования изложена Р. Беллманом в двух формулировках его основной
теоремы.
Первая формулировка: оптимальная стратегия (поведение)
системы не зависит от ее предыстории, а зависит лишь от состояния системы в
данный рассматриваемый момент времени.
Вторая формулировка: если в пространстве состояний системы
некоторым образом построена оптимальная траектория, то любой ее участок,
отсчитываемый от конца, также оптимальная траектория.
Обычная процедура
оптимизации, осуществляемая от начала к концу процесса, сводится к процедуре
поэтапной оптимизации от конца процесса к его началу или, если говорить
формально динамическое
программирование позволяет свести одну сложную задачу со многими переменными ко
многим задачам с малым числом переменных. Это
значительно сокращает объем вычислений и ускоряет процесс принятия управленческого
решения.
В отличие от простого перебора метод динамического программирования дает возможность в отсеивании части решений (траекторий). Например, если известно какое-то допустимое решение и значение критерия на нем, в процессе перебора мы можем не рассматривать те траектории, у которых на предыдущем шаге критерий был выше известного (метод ветвей и границ).
Оптимальную стратегию
управления можно получить, если сначала найти оптимальную стратегию управления
на m – ом шаге, затем на двух
последних шагах, затем на трех последних шагах и т.д., вплоть до первого шага.
Таким образом, решение рассматриваемой задачи динамического программирования
целесообразно начинать с определения оптимального решения на последнем, m –
ом шаге. Для того чтобы найти это решение, очевидно, нужно сделать различные
предположения о том, как мог окончится предпоследний шаг, и с учетом этого
выбрать управление, обеспечивающее максимальное значение функции
Рассмотрим
следующую модель:
i –
индекс объекта (i= 1,…,n);
air –
объем производства продукции по r–ому
варианту на i-ом объекте;
Ai = {ai1……air}-
множество (вариантов) объемов производства на i -ом объекте (r=1,…Ri);
yi –
искомый оптимальный объем производства продукции на i-ом объекте (yi ϵ Ai для i=
1,…,n);
gi(yi) –затраты, связанные с
производством продукции в объеме yi на i-ом объекте;
b –
суммарная потребность в однородной продукции;
Fn(b) – оптимальные суммарные затраты системы
объектов на объем b.
Необходимо удовлетворить потребность
b с минимальными суммарными затратами,
используя возможности рассматриваемых объектов.
Решение модели
методом динамического программирования.
Пусть Fk(b) – оптимальные затраты k предприятий на
производство объёма b. Запишем систему
рекуррентных соотношений, исходя из принципа оптимальности (b – принимает значение в интервале [0; b]):
Fn(b)= ![]()
Fn-1(b)= ![]()
…
F2(b) = ![]()
F1(b) = 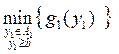
F1(b) = ¥ , если ![]() < b
< b
При расчетах для k предприятий,
если расчетный объем меньше 0, то берется значение оптимальных затрат для 0. Fk (-) = Fk(0)
Пример. Есть 3 предприятия, у каждого
предприятия 3 варианта развития (![]() - объемы производства и
- объемы производства и ![]() затраты). Определить
оптимальные (минимальные) суммарные затраты 3 предприятий для удовлетворения
потребности b = 30 единиц.
затраты). Определить
оптимальные (минимальные) суммарные затраты 3 предприятий для удовлетворения
потребности b = 30 единиц.
|
1 предприятие |
2 предприятие |
3 предприятие |
|||
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
- |
- |
|
5 |
50 |
10 |
85 |
10 |
90 |
|
10 |
90 |
15 |
130 |
20 |
160 |
|
15 |
135 |
20 |
160 |
25 |
190 |
Итак, в качестве первого шага процесса
решения, оценим оптимальные затраты одного (первого) предприятия на расчетный объем. Эти величины
рассчитываются как минимум затрат этого предприятия, при условии, что данный
объем может быть удовлетворен возможностями этого предприятия (в противном
случае, затраты равны бесконечности).
Результаты расчетов будем заносить в
специальным образом организованную таблицу. В качестве расчетных объемов (левый столбец) рассматриваются возможные
значения, которые могут образовываться от сочетания вариантов производства на
предприятиях. Это разбиение конечного спроса на промежуточные значения обычно
не является сложной задачей, в крайнем случае, можно выбрать достаточно дробную
сетку значений. Столбцы F1 и у1 заполняются исходя из
данных по первому предприятию, в соответствии с вышеописанным алгоритмом.
F1(b) = 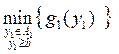
F1(b) = ¥ , если
![]() < b
< b
Результирующая
таблица (с внесенными значениями для 1 объекта)
|
b |
F1 |
y1 |
F2 |
y2 |
F3 |
y3 |
|
0 |
0 |
0 |
|
|
|
|
|
5 |
50 |
5 |
|
|
|
|
|
10 |
90 |
10 |
|
|
|
|
|
15 |
135 |
15 |
|
|
|
|
|
20 |
∞ |
- |
|
|
|
|
|
25 |
∞ |
- |
|
|
|
|
|
30 |
∞ |
- |
|
|
|
|
Оптимальные затраты двух предприятий на расчетный объем рассчитываются как
минимум суммы оптимальных затрат для первого объекта (берётся из таблицы) и
затрат второго предприятия (минимум по «возможностям» 2-го предприятия)
F2(b) = ![]()
Расчеты
удобно проводить, заполняя соответствующие таблицы для каждого расчетного
объема (ниже, для примера, приведены расчеты только для объемов b={0; 5; 25 и
30}). Результаты, заносимые в таблицу, выделены жирным курсивом:
|
b |
y2 |
g2 |
b-y2 |
F1(b-y2) |
F1+g2 |
F2(min) |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
10 |
85 |
-10 |
0 |
85 |
|
|
0 |
15 |
130 |
-15 |
0 |
130 |
|
|
0 |
20 |
160 |
-20 |
0 |
160 |
|
b |
y2 |
g2 |
b-y2 |
F1(b-y2) |
F1+g2 |
F2(min) |
|
5 |
0 |
0 |
5 |
50 |
50 |
50 |
|
5 |
10 |
85 |
-5 |
0 |
85 |
|
|
5 |
15 |
130 |
-10 |
0 |
130 |
|
|
5 |
20 |
160 |
-15 |
0 |
160 |
|
…
|
b |
y2 |
g2 |
b-y2 |
F1(b-y2) |
F1+g2 |
F2(min) |
|
25 |
0 |
0 |
25 |
∞ |
∞ |
|
|
25 |
10 |
85 |
15 |
135 |
220 |
|
|
25 |
15 |
130 |
10 |
90 |
220 |
|
|
25 |
20 |
160 |
5 |
50 |
210 |
210 |
|
b |
y2 |
g2 |
b-y2 |
F1(b-y2) |
F1+g2 |
F2(min) |
|
30 |
0 |
0 |
30 |
∞ |
∞ |
|
|
30 |
10 |
85 |
20 |
∞ |
∞ |
|
|
30 |
15 |
130 |
15 |
135 |
265 |
|
|
30 |
20 |
160 |
10 |
90 |
250 |
250 |
Результирующая
таблица после второго шага:
|
b |
F1 |
y1 |
F2 |
y2 |
F3 |
y3 |
|
0 |
0 |
0 |
0 |
0 |
|
|
|
5 |
50 |
5 |
50 |
0 |
|
|
|
10 |
90 |
10 |
85 |
10 |
|
|
|
15 |
135 |
15 |
130 |
15 |
|
|
|
20 |
∞ |
- |
160 |
20 |
|
|
|
25 |
∞ |
- |
210 |
20 |
|
|
|
30 |
∞ |
- |
250 |
20 |
|
|
Оптимальные затраты трех предприятий на суммарную
потребность рассчитываются как минимум суммы оптимальных затрат двух
предприятий и затрат третьего предприятия (минимум по «возможностям» 3-го
предприятия):
F3(b) = ![]()
Для выбора оптимального значения y3 можно также
воспользоваться вспомогательной таблицей:
|
b |
y3 |
g3 |
b-y3 |
F2(b-y3) |
F2+g3 |
F3(min) |
|
30 |
10 |
90 |
20 |
160 |
250 |
|
|
30 |
20 |
160 |
10 |
85 |
245 |
|
|
30 |
25 |
190 |
5 |
50 |
240 |
190 |
Результирующая таблица после третьего
шага:
|
b |
F1 |
y1 |
F2 |
y2 |
F3 |
y3 |
|
0 |
0 |
0 |
0 |
0 |
|
|
|
5 |
50 |
5 |
50 |
0 |
|
|
|
10 |
90 |
10 |
85 |
10 |
|
|
|
15 |
135 |
15 |
130 |
15 |
|
|
|
20 |
∞ |
- |
160 |
20 |
|
|
|
25 |
∞ |
- |
210 |
20 |
|
|
|
30 |
∞ |
- |
250 |
20 |
190 |
25 |
Чтобы в явном виде представить
полученное решение, надо пройти «обратный» путь. В таблице в последнем столбце
стоит объем производства третьего предприятия– 25 единиц в оптимальном плане и
общие затраты - 190. Двигаясь к началу таблицы, мы должны перейти к предыдущему
предприятию и подняться по вертикали к строке (b - y3) = (30
– 25) = 5, где и стоит объем производства второго предприятия в оптимальном
плане – 0. Сдвигаясь по этой строке влево (b
- y3 - y2) =
(30 – 25 – 0) = 5, получаем объем производства первого предприятия в оптимальном
плане – 5.
Итак, суммарные оптимальные затраты
системы из трех предприятий равны 190. Объем производства первого предприятия –
5 единиц, второе предприятие не вошло в оптимальный план, а на третьем будет выпускаться
25 единиц.
Вышеописанную
однопродуктовую производственную модель можно представить и в виде задачи
целочисленного программирования.
Пусть:
i – индекс объекта (i= 1,…,n);
r – индекс варианта производства продукции (r= 1,…,Ri; i= 1,…,n)
air –
объем производства продукции по r–ому
варианту на i-ом объекте;
сir –
затраты, связанные с производством продукции по r–ому варианту на i-ом
объекте;
b – суммарная потребность в однородной продукции;
zir – интенсивность
использования r–ого варианта на i–ом объекте, при этом zir ϵ {0; 1} .
Тогда однопродуктовую производственную модель в вариантной постановке (с
дискретными переменными) можно записать в следующем виде:
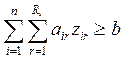
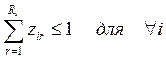
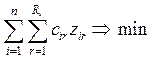
Естественным обобщением этой модели
является многопродуктовая производственная
модель в вариантной постановке (с дискретными переменными).
Пусть:
j – индекс вида продукции (j= 1,…,m);
s – индекс вида ресурса (s= 1,…,k);
i – индекс объекта (i= 1,…,n);
r – индекс варианта производства набора продукции (r= 1,…,Ri; i= 1,…,n)
aijr –
объем производства j –ого вида продукции по r–ому варианту на
i-ом объекте;
qisr – общий объем расхода ресурса s –ого вида при производстве
всех видов продукции по r–ому
варианту на i-ом объекте;
сir – суммарные затраты (валовая
себестоимость), связанные с производством набора продукции по r–ому варианту на i-ом объекте;
b j –
суммарная потребность в продукции j–ого вида;
Qs – общий объем ресурса s–ого
вида, который может быть использован всеми рассматриваемыми объектами;
zir – интенсивность
использования r–ого варианта
производства на i–ом объекте, при
этом zir ϵ {0; 1} .
Тогда:
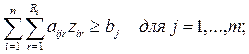
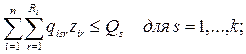
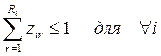
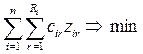
Представим структуру матрицы
коэффициентов этой модели, как задачи целочисленного программирования для
случая: m=2; n=3; k=1 и Ri=2 для всех i .
|
Переменные |
z11 |
z12 |
z21 |
z22 |
z31 |
z32 |
|
|
|
Ограничения
по выпуску продукции |
a111 |
a112 |
a211 |
a212 |
a311 |
a312 |
> |
b1 |
|
a121 |
a122 |
a221 |
a222 |
a321 |
a322 |
> |
b2 |
|
|
Ограничение
по ресурсу |
q111 |
q112 |
q211 |
q212 |
q311 |
q312 |
< |
Q1 |
|
Ограничение
по выбору не более одного варианта производства |
1 |
1 |
|
|
|
|
< |
1 |
|
|
|
1 |
1 |
|
|
< |
1 |
|
|
|
|
|
|
1 |
1 |
< |
1 |
|
|
Коэффициенты
цел. ф-ии |
c11 |
c12 |
c21 |
c22 |
c31 |
c32 |
à |
min |
Производственная
многопродуктовая статическая модель с непрерывными переменными.
а)
с фиксированной структурой производства:
По своей
структуре (структуре матрицы
коэффициентов) данная модель практически полностью совпадает с многопродуктовой
производственной моделью в вариантной постановке (с дискретными переменными),
описанной выше.
Введем
обозначения.
1)
обозначения,
частично совпадающие или модифицированные по содержанию:
j – индекс вида продукции (j= 1,…,m);
s – индекс вида ресурса (s= 1,…,k);
i –
индекс объекта (i= 1,…,n);
r – индекс варианта структуры валового продукта (состава производимой
продукции), (r= 1,…,Ri; i= 1,…,n)
aijr – доля j
–ого вида продукции в общем объеме по r–ому
варианту структуры производства на i-ом объекте;
qisr –
удельные затраты ресурса s –ого
вида при производстве всех видов продукции по r–ому варианту структуры
производства на i-ом объекте;
сir –
суммарные затраты (себестоимость), связанные с производством единицы валовой
продукции по r–ому варианту
структуры на i-ом объекте;
bj –
суммарная потребность в продукции j–ого вида;
Qs – общий объем ресурса s–ого
вида, который может быть использован всеми рассматриваемыми объектами;
zir –
объем валовой продукции произведенной по r–ому варианту структуры на i–ом объекте.
2)
дополнительные
обозначения:
Ni – максимальный суммарный
объем валовой продукции, который может быть произведен на i–ом объекте, с использованием различных структур;
Ni –
минимальный суммарный объем валовой продукции, который должен быть произведен
на i–ом объекте, с использованием
различных структур.
Тогда:
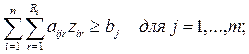
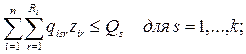
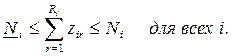
![]()
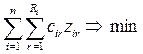
б) с оптимизируемой структурой
производства:
Введем
обозначения.
1)
обозначения,
частично совпадающие или модифицированные по содержанию:
j – индекс вида продукции (j= 1,…,m);
s – индекс вида ресурса (s= 1,…,k);
i –
индекс объекта (i= 1,…,n);
qijs –
удельные затраты ресурса s –ого вида при производстве
единицы
j –ого вида продукции на i-ом
объекте;
сij –
себестоимость производства единицы j –ого вида продукции на i-ом объекте;
bj –
суммарная потребность в продукции j–ого вида;
Qs – общий объем ресурса s–ого
вида, который может быть использован всеми рассматриваемыми объектами;
2)
дополнительные
обозначения:
xij –
объем производства j –ого вида продукции на
действующих мощностях i-ого объекта.
λij – коэффициент использования мощности i-ого объекта при
производстве j –ого вида продукции;
∆xij – объем
производства j –ого вида продукции на вновь вводимых мощностях i-ого объекта.
Ni – максимальный уровень
использования мощности на i–ом
объекте, при производстве различных видов продукции;
Ni– минимальный уровень
использования мощности на i–ом
объекте, при производстве различных видов продукции;
∆Ni–
прирост мощности на i–ом объекте,
используемой при производстве различных видов продукции.
∆сij –
себестоимость производства единицы j –ого вида продукции на
i-ом объекте, с учетом затрат на
увеличение его мощности.
Тогда:
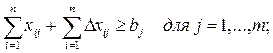
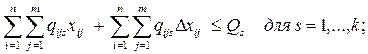
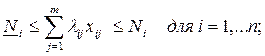
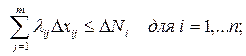
![]()
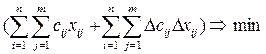
Производственно-транспортные
модели
Модели такого типа являются композицией
представителей ранее рассмотренных двух групп моделей: транспортных (в более
общем случае, транспортно-производственных) и производственных. Условно такое
комбинирование моделей можно представить в виде графической блок-схемы:
|
П1 |
|
|
|
< |
Правая часть
ограничений |
|
|
|
|
= |
||
|
Т1 |
|
|
> |
||
|
|
|
|
< |
||
|
|
П2 |
|
= |
||
|
|
|
|
> |
||
|
|
|
Т2 |
< |
||
|
|
|
|
= |
||
|
|
|
|
> |
||
|
Общие
ограничения |
< |
||||
|
Общая целевая
функция |
à |
extr |
|||
В качестве П1 и П2 могут рассматриваться
производственные модели различного типа – в вариантной постановке (с
дискретными переменными) либо в непрерывной постановке, с фиксированной или
оптимизируемой структурой производства, описанные выше. Под блоками Т1
и Т2 в этой блок-схеме представлены соотношения по перевозке сырь,
ресурсов, промежуточной и конечной
продукции. Конкретное наполнение блоков зависит от экономической постановки
задачи и допускает различные их модификации. В качестве примера рассмотрим
следующую целочисленную производственно-транспортную модель, блок-схема которой
выглядит следующим образом (хотя рассматриваемый алгоритм решения может быть
распространен и на более общий случай):
|
П1 |
|
Правая часть |
|
|
Т1 |
|||
|
|
|||
|
Общая целевая
функция |
extr |
|
|
Целочисленная
производственно-транспортная модель и ее решение «методом отсечений».
Известны пункты возможного размещения
производственных объектов, производящих или потребляющих некоторые продукты.
Каждый объект может развиваться в рассматриваемый промежуток времени по одному
из нескольких возможных для него альтернативных вариантов. Реализация каждого
из вариантов сопряжена с производственными затратами, определенными расчетным
способом. Известны транспортные затраты на перевозки продуктов от одного
объекта к другому или в конечный пункт потребления. Требуется определить
размещение и функционирование производства в пунктах таким образом, чтобы
суммарные производственно-транспортные затраты были минимальными и при этом
выполнялись различного рода дополнительные ограничения. Более точно задача
может быть сформулирована так.
Пусть:
j – индекс вида продукции (j= 1,…,m);
k –
индекс пункта потребления продукции (k= 1,…,K);
i – индекс
производственного объекта (i= 1,…,n);
r – индекс варианта
производства набора продукции
(r=
1,…,Ri; i= 1,…,n);
aijr –
объем производства j –ого вида продукции по r–ому варианту на
i-ом объекте;
сir – суммарные затраты (валовая
себестоимость), связанные с производством набора продукции по r–ому варианту на i-ом объекте;
tijk –
затраты на перевозку единицы продукции j–ого вида от i-ого производственного объекта в k–ый пункт потребления;
bjk –
суммарная потребность в продукции j–ого вида в k –ом
пункте;
zir – искомая интенсивность
использования r–ого варианта
производства на i–ом объекте, при
этом zir ϵ {0; 1}.
Если в решении zir =
1, то вариант входит в оптимальный план, а zir = 0
означает, что не входит. При этом по каждому объекту может быть задействовано
не более одного варианта.
xijk – искомый объем перевозки продукции j–ого
вида от i-ого производственного объекта
в k–ый пункт
потребления.
Тогда модель
запишется следующим образом:
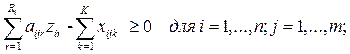
(А1)
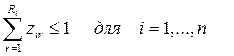 (А2)
(А2)
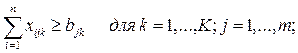 (А3)
(А3)
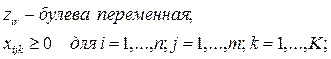 (А4)
(А4)
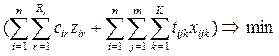 (А5)
(А5)
Пара <z, x> называется производственно-транспортным планом,
если z удовлетворяет
условиям (А1) - (А5). При этом z
называется производственной составляющей
(производственным планом), а x —
транспортной составляющей (транспортным планом). Слагаемые целевой функции (1)
и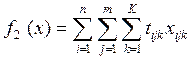
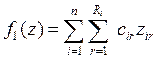
отражают соответственно производственные и
транспортные затраты по реализации плана <z, x>.
Производственно-транспортный план называется
допустимым, если он удовлетворяет условиям (А1) - (А4) и оптимальным, если,
кроме того, доставляет минимум функции (А5).
Задача (А1) - (А5) является задачей частично
целочисленного линейного программирования и обладает рядом специфических
особенностей:
1) каждая
переменная вида xijk входит
только в два ограничения, причем в одно из ограничений с коэффициентом +1, а в
другое — с коэффициентом —1;
2)
совокупность переменных xijk распадается на несколько групп по количеству производимых
видов продукции;
3)
целочисленные переменные могут принимать лишь два значения - 0 или 1;
4) множество
целочисленных переменных разбито на непересекающиеся группы (по количеству
пунктов производства), в каждой из которых лишь одна переменная может быть
отлична от нуля.
Такого рода модели известны в литературе под
названием производственно-транспортных моделей в вариантной постановке или
целочисленных производственно-транспортных моделей. Они широко используются при
решении задач размещения и развития предприятий отраслей на перспективу. Для
численных расчетов таких моделей предложены различные методы.
Перейдем к изложению метода (полное описание этого
метода можно найти в [ ]). Здесь же приведем только последовательность расчетов
с небольшими комментариями относительно сходимости, а также проиллюстрируем его
на конкретном примере.
Разобьем исходную модель на две составляющие:
производственную и транспортную. При этом в качестве нагрузки (конечной
потребности) будем рассматривать суммарный спрос по каждому виду продукции.
Итак, производственную модель можно записать
следующим образом:
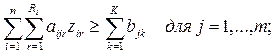
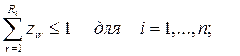
![]()
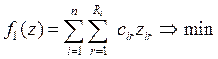
Если решение данной модели существует (иначе и
исходная производственно-транспортная модель не имеет решения), то можно
сформировать m (по количеству продуктов) транспортных задач, где в
качестве объемов поставок использовать те объемы производства, которые
выбрались в производственной модели представленной выше.
Пусть
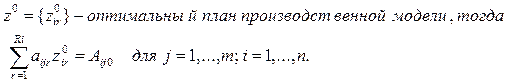 Aij0 - объемы производства j –ого
вида продукции на i-ом
производственном объекте и можно сформировать m транспортных задач следующего вида:
Aij0 - объемы производства j –ого
вида продукции на i-ом
производственном объекте и можно сформировать m транспортных задач следующего вида:
Для ![]()
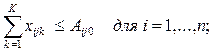
B1)
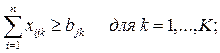 (B2)
(B2)
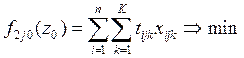
Суммарные (производственные и транспортные) затраты
на этом шаге, после решения серии транспортных задач, составят:
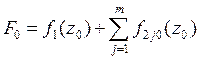
Алгоритм предполагает построение последовательности
таких производственных планов, для которых сумма производственных и
транспортных затрат минимальна. Так как полученный на первом шаге производственный
план является лучшим с позиции затрат на производство продукции, улучшение этой
суммы можно достичь только «ухудшая» производственный план, но при этом получая
большую экономию на транспортных затратах.
Рассматриваемые ниже способы исключения
«неперспективных» (не приводящим к существенной экономии транспортных затрат)
производственных планов основаны на использовании двойственно допустимых систем
потенциалов транспортных задач. С их помощью формируются дополнительные
линейные ограничения (отсечения). Если производственный план не удовлетворяет
какому-либо из таких ограничений, то он заведомо является неперспективным и
может быть исключен (соответствующие
транспортные задачи не решаются).
Пусть:
F* -
суммарные (производственные и транспортные) затраты на этом текущем шаге, после
решения серии транспортных задач,
uij - двойственная переменная транспортной задачи,
соответствующая ограничениям (B1) на этом же
шаге;
vjk - двойственная переменная транспортной задачи,
соответствующая ограничениям (B2) на этом же
шаге.
Запишем суммарное значение затрат используя
двойственное представление функционалов транспортных задач:
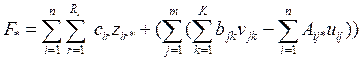
Введем следующее ограничение (для поиска
«перспективного» производственного плана):
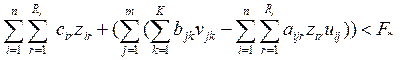
приведя
подобные и перенеся независящие от выбора производственного плана слагаемые в
правую часть соотношения:
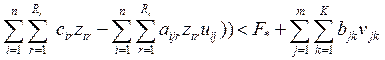
или
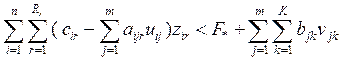 (A)
(A)
Отметим, что величина
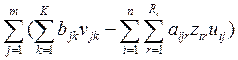
представляет
собой оценку транспортных затрат «снизу» для
транспортного плана x(z) (если
последний существует). Это является следствием того, что допустимость (но не
оптимальность) решений двойственных транспортных задач:
![]()
не
зависит от выбора производственного плана.
Заметим, что от строгих неравенств в (A) нетрудно
перейти к неравенствам со знаком « < » (это может
потребоваться при использовании программ оптимизации для отыскания
производственных планов). Так как
zir ϵ {0; 1} булевы переменные, то всегда найдется ![]() число ᶓ > 0 такое, что множества производственных
планов, удовлетворяющих соотношениям (A) и (A6)
число ᶓ > 0 такое, что множества производственных
планов, удовлетворяющих соотношениям (A) и (A6)
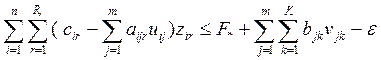 (A6)
(A6)
будут
совпадать.
Проиллюстрируем основные идеи метода на примере
решения однопродуктовой производственно-транспортной задачи с дискретными
(булевыми) переменными в производственном блоке. Отметим, что движение к
оптимальному производственно-транспортному плану осуществляется по множеству
производственных планов, для которых решаются транспортные задачи. Системы
потенциалов, получаемые в результате решения транспортных задач, служат для
построения дополнительных линейных ограничений (отсечений), которые
используются для отсева «неперспективных» производственных планов.
Пример.
Есть 3 предприятия, у каждого предприятия 3 варианта развития
(![]() - объемы производства по вариантам
- объемы производства по вариантам
![]() - соответствующие затраты),
причем второе предприятие должно обязательно входить в план.
- соответствующие затраты),
причем второе предприятие должно обязательно входить в план.
|
Предприятие
№1 |
Предприятие
№2 |
Предприятие
№3 |
|||
|
|
|
|
|
|
|
|
5 |
50 |
10 |
85 |
10 |
80 |
|
10 |
90 |
15 |
130 |
20 |
150 |
|
15 |
135 |
20 |
160 |
25 |
190 |
Имеются 3 потребителя продукции с
фиксированными потребностями {15; 5; 10},
также фиксированы транспортные затраты на перевозку от предприятий к потребителям.
|
|
Объемы потребления и |
||
|
15 |
5 |
10 |
|
|
Предприятие
№1 |
3 |
9 |
6 |
|
Предприятие
№2 |
2 |
5 |
16 |
|
Предприятие
№3 |
5 |
11 |
9 |
Необходимо выбрать варианты развития предприятий и
прикрепить к ним потребителей так, чтобы потребности были полностью
удовлетворены, а суммарные производственно-транспортные затраты были минимальными.
Шаг 1. Выделяем из общей задачи производственный блок (в
качестве ограничения по производству берем сумму объемов потребления).
Определить какие предприятия, и с какими вариантами
развития обеспечат необходимый суммарный объем потребления 30 единиц при
минимальных производственных затратах.
Решаем производственную целочисленную задачу (либо средствами Excel - процедура
«Поиск решения или «Solver» в англоязычной версии, либо используя метод
динамического программирования).
Матрица коэффициентов производственной задачи (такое
представление задачи удобно для использования средств оптимизации в Excel) будет следующей:
|
Переменные |
z11 |
z12 |
z12 |
z21 |
z22 |
z12 |
z31 |
z32 |
z12 |
|
|
|
Производство |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
> |
30 |
|
Ограничения
на выбор вариантов |
1 |
1 |
1 |
|
|
|
|
|
|
< |
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
< |
1 |
|
|
Целевая
функция |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
à |
min |
А оптимальное решение этой задачи:
|
Переменные |
z11 |
z12 |
z12 |
z21 |
z22 |
z12 |
z31 |
z32 |
z12 |
|
Коэффициенты
целевой функции |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
|
Значения переменных |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
\Объемы
производства |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
Оптимальные производственные затраты на
этой итерации П0 =
235
Шаг 2. Определяем объемы производства Ai0 = {0; 10; 20} и формируем транспортную задачу. Соответствующая
транспортная задача имеет следующее решение:
|
Первая итерация |
Объемы потребления и |
ui |
|||
|
15 |
5 |
10 |
|
||
|
Предприятие
№1 |
0 |
0 |
0 |
0 |
3 |
|
Предприятие
№2 |
10 |
5 |
5 |
0 |
3 |
|
Предприятие
№3 |
20 |
10 |
0 |
10 |
0 |
|
vk |
5 |
8 |
9 |
|
|
А транспортные
затраты Т0 = 175.
Формируем
дополнительное ограничение (отсечение). Рассчитаем правую часть ограничения:
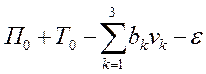 ПЧ =
ПЧ =
В качестве ᶓ
можно взять 1 (подстановки переменных в левую часть отсечения дают
значения, отличающиеся на большую величину). Итак,
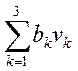
Сумма
функционалов = 235+175 = 410 = 5*15+8*5+9*10 =
205 àПЧ= 410-205-1.
А коэффициенты
отсечения равны сir - air* ui
|
С=
{сir} |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
||
|
A= {air} |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
||
|
U= {ui} |
3 |
3 |
3 |
3 |
3 |
3 |
0 |
0 |
0 |
ПЧ |
|
|
(C-UA)Z<ПЧ |
35 |
60 |
90 |
55 |
85 |
100 |
80 |
150 |
190 |
< |
204 |
Переходим
к следующей итерации, повторим Шаг 1
и Шаг 2.
Матрица
коэффициентов производственной задачи на второй итерации:
|
Переменные |
z11 |
z12 |
z12 |
z21 |
z22 |
z12 |
z31 |
z32 |
z12 |
|
|
|
Производство |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
> |
30 |
|
Ограничения
на выбор вариантов |
1 |
1 |
1 |
|
|
|
|
|
|
< |
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
< |
1 |
|
|
Отсечение 1 |
35 |
60 |
90 |
55 |
85 |
100 |
80 |
150 |
190 |
< |
204 |
|
Целевая
функция |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
à |
min |
А оптимальное решение этой задачи:
|
Переменные |
z11 |
z12 |
z12 |
z21 |
z22 |
z12 |
z31 |
z32 |
z12 |
|
Значения переменных |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
\Объемы производства |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
Оптимальные производственные затраты на
этой итерации П1 =
240
Шаг 2. Объемы производства Ai1 = {0; 20; 10} Соответствующая транспортная задача
имеет следующее решение:
|
Первая итерация |
Объемы потребления и |
ui |
||||
|
15 |
5 |
10 |
|
|||
|
Предприятие
№1 |
0 |
0 |
0 |
0 |
3 |
|
|
Предприятие
№2 |
20 |
15 |
5 |
0 |
0 |
|
|
Предприятие
№3 |
10 |
0 |
0 |
10 |
0 |
|
|
Т1= 145 |
vk |
2 |
5 |
9 |
|
|
Формируем
дополнительное ограничение (отсечение). Рассчитаем правую часть ограничения: ПЧ=
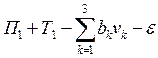 , В
качестве ᶓ можно взять 1
(подстановки переменных в левую часть отсечения дают значения, отличающиеся на
большую величину). Итак,
, В
качестве ᶓ можно взять 1
(подстановки переменных в левую часть отсечения дают значения, отличающиеся на
большую величину). Итак,
![]() = 240+145 = 385
= 240+145 = 385 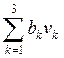 = 2*15+5*5+9*10 = 145 àПЧ= 385-145-1.
= 2*15+5*5+9*10 = 145 àПЧ= 385-145-1.
А коэффициенты
отсечения равны сir - air* ui
|
С=
{сir} |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
||
|
A= {air} |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
||
|
U= {ui} |
3 |
3 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
ПЧ |
|
|
(C-UA)Z<ПЧ |
35 |
60 |
90 |
85 |
130 |
160 |
80 |
150 |
190 |
< |
239 |
Переходим к
следующей итерации, повторим Шаги 1 и 2.
Шаг 1. Решение
производственной задачи на третьей итерации:
Матрица
коэффициентов производственной задачи на третьей итерации:
|
Переменные |
z11 |
z12 |
z12 |
z21 |
z22 |
z12 |
z31 |
z32 |
z12 |
|
|
|
Производство |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
> |
30 |
|
Ограничения
на выбор вариантов |
1 |
1 |
1 |
|
|
|
|
|
|
< |
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
< |
1 |
|
|
Отсечение 1 |
35 |
60 |
90 |
55 |
85 |
100 |
80 |
150 |
190 |
< |
204 |
|
Отсечение 2 |
35 |
60 |
90 |
85 |
130 |
160 |
80 |
150 |
190 |
< |
239 |
|
Целевая
функция |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
à |
min |
|
Решение: |
|
\Переменные |
|
z11 z12 z13 z21 z22 z23 z31 z32 z33 Значения переменных 0 1 0 0 0 1 0 0 0 \Объемы
производства 5 10 15 10 15 20 10 20 25 |
Оптимальные производственные затраты на
этой итерации П2 =
250
Шаг 2. Объемы производства Ai2 = {10; 20; 0}
Решение транспортной задачи:
|
Первая итерация |
Объемы потребления и |
ui |
||||
|
15 |
5 |
10 |
|
|||
|
Предприятие
№1 |
0 |
0 |
0 |
10 |
0 |
|
|
Предприятие
№2 |
20 |
15 |
5 |
0 |
0 |
|
|
Предприятие
№3 |
10 |
0 |
0 |
0 |
0 |
|
|
Т2= 115 |
vk |
2 |
5 |
9 |
|
|
Формируем
дополнительное ограничение (отсечение).
Рассчитаем
правую часть ограничения: ПЧ= 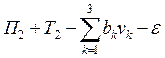 , ᶓ =1 (смотри замечание на предыдущих
итерациях). Итак,
, ᶓ =1 (смотри замечание на предыдущих
итерациях). Итак,
![]() = 250+115 = 365
= 250+115 = 365 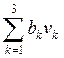 = 2*15+5*5+9*10 = 115 àПЧ= 365-115-1.
= 2*15+5*5+9*10 = 115 àПЧ= 365-115-1.
А коэффициенты
отсечения равны сir - air* ui
|
С=
{сir} |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
||
|
A= {air} |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
||
|
U= {ui} |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
ПЧ |
|
|
(C-UA)Z<ПЧ |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
< |
249 |
Переходим к
следующей итерации, повторим Шаги 1 и 2. При
этом Шаг 2 выполняется
только в том случае, если соответвующая
производственная задача с добавленными отсечениями имеет решение.
Шаг 1. Решение
производственной задачи на третьей итерации:
Матрица
коэффициентов производственной задачи на третьей итерации:
|
Переменные |
z11 |
z12 |
z12 |
z21 |
z22 |
z12 |
z31 |
z32 |
z12 |
|
|
|
Производство |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
> |
30 |
|
Ограничения на выбор вариантов |
1 |
1 |
1 |
|
|
|
|
|
|
< |
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
< |
1 |
|
|
Отсечение 1 |
35 |
60 |
90 |
55 |
85 |
100 |
80 |
150 |
190 |
< |
204 |
|
Отсечение 2 |
35 |
60 |
90 |
85 |
130 |
160 |
80 |
150 |
190 |
< |
239 |
|
Отсечение 3 |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
< |
249 |
|
Целевая
функция |
50 |
90 |
135 |
85 |
130 |
160 |
80 |
150 |
190 |
à |
min |
Решение данной задачи не существует, что означает
отсутствие «перспективных» производственных планов, позволяющих получить
выигрыш в суммарных затратах за счет снижения транспортной составляющей. Это
является признаком окончания расчетов по данному алгоритму.
Среди ранее найденных производственных и
транспортных планов есть пара решений с наименьшими суммарными
производственно-транспортными затратами. Выпишем значения суммарных затрат по
итерациям:
![]() = 235 + 175 = 410;
= 235 + 175 = 410;
![]() = 240 + 145 = 385;
= 240 + 145 = 385;
![]() = 250 + 115 = 365.
= 250 + 115 = 365.
То есть оптимальное решение было достигнуто на
последней итерации.
Оптимальное решение производственной задачи:
|
Переменные |
z11 |
z12 |
z13 |
z21 |
z22 |
z23 |
z31 |
z32 |
z33 |
|
Значения переменных |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
Объемы
производства |
5 |
10 |
15 |
10 |
15 |
20 |
10 |
20 |
25 |
Решение
транспортной задачи:
|
|
15 |
5 |
10 |
ui |
||
|
Предприятие
№1 |
0 |
0 |
0 |
10 |
0 |
|
|
Предприятие
№2 |
20 |
15 |
5 |
0 |
0 |
|
|
Предприятие
№3 |
10 |
0 |
0 |
0 |
0 |
|
|
|
vk |
2 |
5 |
9 |
|
|
Производственные
многопродуктовые динамические модели.
Возможны два подхода к взаимной увязке в
моделях последовательных во времени состояний производственных объектов.
Первый подход выражается в
том, что способы функционирования объектов формируются как «сквозные» и описывают
развитие объекта во времени в разрезе выделенных моментов времени. Показатели
целевой функции (например затраты) в этом случае исчисляются как интегральные,
т.е. суммарные за весь плановый период (при этом разновременные затраты
приводятся к одному периоду времени).
При втором подходе способы
функционирования формируются так, что каждый из них описывает состояние объекта
только в одном из выделенных моментов времени. Показатели целевой функции
(например, затраты) здесь исчисляются для каждого из выделенных моментов
времени, но в общем критерии оптимизации эти показатели соответствующим образом
дисконтируются. Взаимная непротиворечивость таких способов во времени
обеспечивается включением в модель дополнительных ограничений и способов согласования состояний объекта в
последовательных моментах времени периода прогнозирования.
Запишем модель со «сквозными» способами
функционирования объектов и фиксированной структурой производства в течении
каждого периода времени (с непрерывными переменными).
К обозначениям, введенным при описании
статических производственных моделей, добавляется индекс ![]() , характеризующий порядковый номер выделенного момента
времени (месяца, года или иного интервала времени) периода прогнозирования.
, характеризующий порядковый номер выделенного момента
времени (месяца, года или иного интервала времени) периода прогнозирования.
В принятых обозначениях задача сводится
к следующему:
найти
такие значения переменных ![]() при которых минимизируется
(максимизируется) величина целевой функции
при которых минимизируется
(максимизируется) величина целевой функции
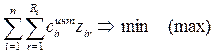
При условиях:
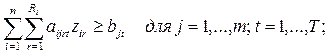
- объекты системы в каждом периоде
прогнозирования в совокупности суммарно должны произвести не меньше заданных
для этого момента объемов продукции;
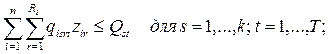
- система рассматриваемых объектов в
каждом периоде прогнозирования может использовать не больше имеющихся в этот
момент времени (году) ресурсов s– го вида;
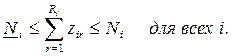
- валовой объем производства на каждом
объекте ограничен. Возможные траектории развития объектов формируются в виде
набора двух множеств параметров: {![]() } и {
} и {![]() }, в вариации которых может быть заложены варианты
динамики развития. Особое значение при разработке динамики производства
продукции и использования ресурсов следует уделять учету лагов в создании
фондов (в качестве ресурсов могут выступать инвестиции), а также наращиванию
объемов производства в связи с освоением (вводом в действие) ресурсов производственной
инфраструктуры. Отметим также, что среди ресурсов могут выделяться как локальные,
относящиеся к одному или группе объектов, так и глобальные, относящиеся ко всей
системе в целом.
}, в вариации которых может быть заложены варианты
динамики развития. Особое значение при разработке динамики производства
продукции и использования ресурсов следует уделять учету лагов в создании
фондов (в качестве ресурсов могут выступать инвестиции), а также наращиванию
объемов производства в связи с освоением (вводом в действие) ресурсов производственной
инфраструктуры. Отметим также, что среди ресурсов могут выделяться как локальные,
относящиеся к одному или группе объектов, так и глобальные, относящиеся ко всей
системе в целом.
Динамические модели в вариантной
постановке (с дискретными переменными) со сквозными способами по структуре не
отличаются от вышеописанной модели с непрерывными переменными. Основное отличие
связано с расчетом параметров, которые относятся к объемам производства
продукции и потребления ресурсов, а не являются удельными показателями.
Дискретность переменных модели позволяет учесть нелинейный характер
зависимость, но затрудняет численную реализацию.
Для дискретных моделей (производственных
задач в вариантной постановке) рассмотрим введение так называемых «составных
способов», каждый из которых описывает функционирование объекта в
течение года.
Тогда цель оптимизации сводится к поиску
экстремума функционала
![]()
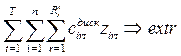
При условиях:
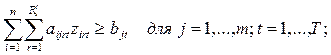
- объекты системы в каждом периоде прогнозирования
в совокупности суммарно должны произвести не меньше заданных для этого момента
объемов продукции;
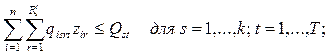
- система рассматриваемых объектов в
каждом периоде прогнозирования может использовать не больше имеющихся в этот
момент времени (году) ресурсов s– го вида;
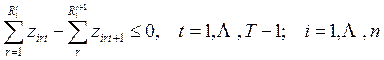
- интенсивность использования
производственного объекта по интервалам планового периода не убывает;
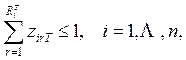
-условия выбора не более одного варианта
в последнем плановом интервале;
zirt ϵ {0; 1} для r = 1,…,![]() ; i=1,…,n; t = 1,…,T;
; i=1,…,n; t = 1,…,T;
- условия альтернативного выбора
варианта функционирования объекта.
В данной модели предполагается
отсутствие зависимости между вариантами функционирования объекта в разные
интервалы времени, т.е. ингредиенты «составных способов» не корректируются в
зависимости от той или иной комбинации способов, вошедших в оптимальный план в
предыдущем интервале времени.
Переход от динамической производственной
модели к производственно-транспортной достаточно прост. Например, типичной
моделью с добавленным транспортным блоком является следующая модификация
описанной выше динамической производственной задачи в вариантной постановке
(динамика представлена «составными
способами»):
![]()
![]() -
индекс пункта потребления готовой продукции (
-
индекс пункта потребления готовой продукции (![]() );
);
![]() -объем
потребления
-объем
потребления ![]() -го
вида продукции в
-го
вида продукции в ![]() -м пункте;
-м пункте;
![]() -
объем поставок j-го
вида продукции из i-го пункта в l-ый;
-
объем поставок j-го
вида продукции из i-го пункта в l-ый;
![]() -
соответствующие дисконтированные затраты на поставку j-го вида продукции
из i-го пункта в l-ый.
-
соответствующие дисконтированные затраты на поставку j-го вида продукции
из i-го пункта в l-ый.
Если критерием является минимизация
затрат, то требуется минимизировать
При
условиях:
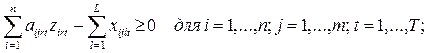
-
объекты системы в каждом периоде прогнозирования должны произвести не меньше
вывозимых объемов продукции;
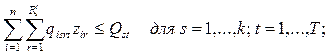
-
система рассматриваемых объектов в каждом периоде прогнозирования может
использовать не больше имеющихся в этот момент времени (году) ресурсов s– го вида;
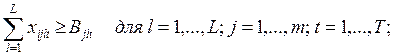
-
в каждый пункт потребления должно быть ввезено достаточное количество
продукции;
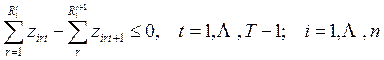
-
интенсивность использования производственного объекта по интервалам планового
периода не убывает;
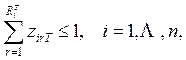
-условия
выбора не более одного варианта в последнем плановом интервале;
zirt ϵ {0; 1} и ![]() для r = 1,…,
для r = 1,…,![]() ;
i=1,…,n; t = 1,…,T; l=1,…,L
;
i=1,…,n; t = 1,…,T; l=1,…,L
-
условия альтернативного выбора варианта функционирования объекта и неотрицательности поставок продукции.
Оптимизация
отраслевых систем в условиях неопределенности
Существенной особенностью сложных экономических систем (народного хозяйства в целом, его территориальных и отраслевых подсистем) является то, что их функционирование не допускает жесткого детерминированного описания из-за чрезвычайного многообразия внутренних и внешних связей, участия в процессе их взаимодействия активных элементов, поведение которых не может быть однозначно предопределено или предсказано. Эти системы осуществляют свое закономерное развитие лишь в виде тенденции, постоянно нарушаемой под влиянием случайных факторов, т.е. обладают вероятностными свойствами, определяющими невозможность однозначного предсказания условий и оптимальных направлений их будущего развития. Таким образом, фактор неопределенности – один из важнейших, который надо учитывать при управлении экономическими системами.
Наличие вероятностных свойств обуславливает существование зоны неопределенности оптимального развития экономических систем, т.е. некоторой совокупности вариантов их развития, каждый из которых является оптимальным при каких либо реальных сочетаниях исходных данных. Вследствие этого подлинной задачей оптимизации перспективного развития любой экономической системы необходимо считать не определение одного оптимального решения, а выделение и всестороннюю экономическую оценку всей совокупности оптимальных вариантов, образующих зону неопределенности ее развития.
Рассмотрим один из возможных подходов к оптимизации отраслевых систем в условиях неполноты исходной информации. Предлагаемый подход основан на использовании детерминированных математических моделей экономических систем, сводящихся к общей задаче линейного программирования, хотя в принципе может быть реализован на нелинейных и дискретно-нелинейных моделях.
Он предусматривает имитацию на ЭВМ множества возможных условий развития экономической системы. Это достигается изменением значений функционала и вектора ограничений, т.е. экономических и натуральных показателей системы в пределах предполагаемого интервала погрешности. Различные случайные сочетания значений коэффициентов функционала и вектора ограничений имитируют колебания реальных условий, а решения, полученные при реализации модели для каждого сочетания, характеризуют возможные оптимальные способы развития системы и в своей совокупности – зону ее неопределенности.
Этот подход, достаточно очевидный по
своей идее, весьма сложен в практической реализации. Во-первых, он требует
формирования достаточно представительного множества сочетаний исходных данных.
Во-вторых, для всех таких сочетаний необходимо найти оптимальные способы
развития системы и на основе их анализа выявить совокупность оптимальных
вариантов, образующих зону неопределенности. В-третьих, требуется дать
экономическую оценку выявленных оптимальных вариантов при различных условиях
развития системы и, что, по-видимому, самое трудное, принять решение по
развитию системы в условиях неопределенности.
В математическом отношении метод
представляет собой синтез
а)
метода статистических испытаний (Монте-Карло),
б) приемов корректировки оптимального решения задачи линейного программирования при изменении первоначальных исходных данных,
в) методов распознавания образов,г) аппарата принятия
решений в условиях неопределенности (теория игр).
Рассматривая соответствие данного метода
различным постановкам задачи стохастического программирования, следует сказать,
что он применим лишь к задачам с так называемой «нежесткой»постановкой
, когда выбираемое оптимальное решение может оказаться недопустимым
(неудовлетворяющим всем или некоторым ограничениям задачи) при каких либо
реально возможных сочетаниях исходных данных. По нашему мнению, именно эта
постановка в наибольшей мере отвечает природе и способам проявления фактора
неопределенности в экономических системах, которые, как правило, в состоянии
компенсировать соответствующие рассогласования с помощью резервов продукции и
мероприятий по форсированию (или замораживанию) производственных мощностей.
«Жесткая» же постановка задачи стохастического программирования требует
допустимости (иногда с заданной вероятностью) выбираемого оптимального решения
при всех сочетаниях исходных данных.
Это влечет за собой перерасход затрат на
развитие экономических систем ввиду необходимости выбирать их план по наиболее
неблагоприятным условиям без учета возможности создания и использования резервов.
Предлагаемый метод можно рассматривать как развитие двухэтапного подхода
Данцига - Маданского[1]
применительно к решению задач в условиях неопределенности, причем не только при
изменении вектора ограничений, но и в случае варьирования коэффициентов
функционала. Ниже последовательно рассматриваются основные его этапы.
|
Составление и расчет детерминированной
модели системы |
|
|
|
|
|
Формирование представительной
совокупности M случайных
сочетаний исходных данных методом статистических испытаний |
|
|
Случайные сочетания коэффициентов
функционала |
Случайные сочетания коэффициентов
вектора ограничений |
|
|
|
|
Группировка М случайных сочетаний
исходных данных в заданное количество групп N с помощью методов распознавания образов |
|
|
|
|
|
Получение набора N оптимальных решений |
|
|
При изменении коэффициентов
функционала |
При изменении коэффициентов
вектора ограничений |
|
|
|
|
Выявление набора оптимальных
планов R (зоны неопределенности )путем группировки N оптимальных решений с помощью методов распознавания
образов |
|
|
|
|
|
Проверка достаточности принятого
числа сочетаний исходных данных |
|
|
|
Да |
|
Составление и исследование
адаптивной математической модели системы для приспособления каждого из R вариантов к N различным сочетаниям исходных данных |
|
|
|
|
|
Построение матрицы значений
экономического ущерба от неполного значения будущих условий развития системы |
|
|
|
|
|
Применение различных критериев
принятия решения в условиях неопределенности для отбора равноэкономичных
вариантов развития системы |
|
|
|
|
|
Эвристический анализ равноэкономичных вариантов и рекомендация окончательного
решения |
|
Имитация
реальных условий развития системы
Получение вариантов, формирующих зону
неопределенности развития системы.
Формирование набора случайных исходных
данных(N) является имитацией множества возможных условий
развития системы. Для определения оптимального поведения системы в этих
условиях необходимо решить N
детерминированных экстремальных задач.
При использовании линейных моделей одним
из способов реализации предлагаемого метода является применение алгоритмов
корректировки оптимального решения задачи линейного программирования при
изменении коэффициентов функционала и вектора ограничений.
Для выявления совокупности оптимальных
вариантов в методе вводится деление параметра системы (переменных модели) на существенные, определение которых
собственно и является задачей оптимизации перспективного развития системы (применительно
к топливно-энергетическому комплексу страны –это размеры добычи и межрайонного
распределения основных видов топлива); второстепенные,
которые в модели учитываются лишь для того, чтобы правильно принять решение по
существенным параметрам и подлежат уточнению на последующих стадиях оптимизации.(в
нашем примере – размеры складов топлива и другие режимные характеристики.)
Очевидно что к одному и тому же
оптимальному варианту развития системы должны относится решения с одинаковым
составом существенных параметров.
Однако совпадение состава существенных
параметров является необходимым, но не достаточным условием группировки решений
в оптимальные варианты. Важно учитывать также количественные различия значений
существенных переменных. С этой целью повторно используется специальный
алгоритм распознавания образов – на этот раз для группировки N оптимальных решений, заданных на множестве существенных
переменны, в заранее неизвестное (рациональное) количество оптимальных
вариантов.
В результате применения изложенного
способа группировки множество оптимальных решений N
заменяется равноценной, но гораздо меньшей совокупностью (R<<N) оптимальных
вариантов, которые образуют зону неопределенности развития системы.
Экономическая оценка оптимальных вариантов в
пределах зоны неопределенности.
Полученная на предыдущем этапе зона
неопределенности представляет собой совокупность качественно различных
вариантов развития системы. Очевидно, эти варианты не являются экономически
равноценными. Поэтому возникает необходимость экономической оценки и сравнения
вариантов в пределах зоны неопределенности.
Как известно, при детерминированном
подходе для экономической оценки вариантов используется величина приведенных
затрат (Фn) на развитие и эксплуатацию системы при
одинаковых условиях (n) – потребности
в продукции, ограничениях на ресурсы, экономических показателей объектов и т.п.
Именно по критерию минимума приведенных затрат выявляется зона неопределенности
оптимального развития системы.
Однако для экономической оценки и
последующего сравнения вариантов в пределах зоны неопределенности показатель
суммарных затрат должен применятся в существенно модифицированном виде. В условиях
неопределенности для каждого варианта (r)
должно выполняться не одно значение экономического показателя, а множество
значений (![]() ) - по числу рассмотренных условий развития
системы.
) - по числу рассмотренных условий развития
системы.
Трудность вычисления показателей (![]() ) состоит в том, что наряду с собственными
затратами (
) состоит в том, что наряду с собственными
затратами (![]() ) (соответствующими тем сочетаниям исходных данных, при
которых этот вариант является оптимальным) они включают затраты (
) (соответствующими тем сочетаниям исходных данных, при
которых этот вариант является оптимальным) они включают затраты (![]() ), возникающие в случае реализации варианта в тех или
иных неоптимальных для него условиях (n). Например,
если вариант развития энергосистемы оптимален при среднем потреблении
электроэнергии, то в случае реализации пониженного уровня электропотребления в
системе возможна экономия затрат за счет отказа от строительства некоторой
части намечаемых или сооружаемых энергетических объектов. При повышенной же
потребности либо потребуется проведение экстренных и поэтому чрезмерно дорогих
дополнительных мероприятий по «доразвитию»
производственных мощностей, либо понадобится учитывать ущерб у потребителей от недоотпуска электроэнергии.
), возникающие в случае реализации варианта в тех или
иных неоптимальных для него условиях (n). Например,
если вариант развития энергосистемы оптимален при среднем потреблении
электроэнергии, то в случае реализации пониженного уровня электропотребления в
системе возможна экономия затрат за счет отказа от строительства некоторой
части намечаемых или сооружаемых энергетических объектов. При повышенной же
потребности либо потребуется проведение экстренных и поэтому чрезмерно дорогих
дополнительных мероприятий по «доразвитию»
производственных мощностей, либо понадобится учитывать ущерб у потребителей от недоотпуска электроэнергии.
Отсюда непосредственно следует, что
оптимизация детерминированных моделей в условиях неопределенности является не
более чем вспомогательным этапом для выявления состава вариантов, образующих зону
неопределенности развития системы. Для выбора же наилучшего решения в этих
условиях необходимо выполнить значительно более сложную работу по
приспособлению (адаптации) вариантов к различным условиям развития системы и их
экономической оценке в пределах зоны неопределенности.
По нашему мнению, процесс адаптации
должен включать в себя следующие стадии[2]:
1. Фиксирование варианта развития
системы, т.е. задание состава и диапазона изменения значений существенных
параметров.
2. Определение набора дополнительных («подстроечных») мероприятий, необходимых для адаптации
заданного варианта к различным условиям развития системы.
3. Учет реального процесса уточнения
исходной информации.
4. Определение для каждого варианта оптимального состава «подстроечных» мероприятий
Очевидно, что эффективная реализация
перечисленных требований в едином комплексе невозможна без создания специальной
адаптивной математической модели.
К моделям такого типа предъявляются
более высокие требования, чем к детерминированным моделям, используемым для
выявления оптимальных вариантов, формирующих зону неопределенности развития системы.
Однако они имеют одно важное преимущество, существенно облегчающее их создание
и применение, — задание варианта развития системы и оптимизация в тех или иных
неоптимальных для него условиях сравнительно небольших его корректировок.
Разработанная в СЭИ упрощенная
адаптивная модель в принципе соответствует модели второго этапа двухэтапного
подхода Данцига-Маданского. В отличие от последней,
адаптивная модель не фиксирует жестко значения всех переменных в рассматриваемом
варианте, а делает это лишь для основных (существенных) переменных и только на
начальных этапах расчетного периода. Далее, она позволяет учитывать процесс
уточнения исходной информации, что совсем не предусмотрено в методе Данцига-Маданского. Наконец, адаптивная модель реализуется
существующими вычислительными средствами, в то время как методом Данцига-Маданского до сих пор удавалось решать лишь задачи с
заведомо упрощенной структурой модели второго этапа.
Адаптивная модель строится на базе той
детерминированной модели, с помощью которой выявляется зона неопределенности
оптимального развития системы, целиком и без каких бы то ни было изменений
включает все ее уравнения и переменные. Это обеспечивает правильное описание в
адаптивной модели динамики основных объектов .и связей в пределах всего расчетного
периода.
В качестве первого важного дополнения
адаптивная модель включает ограничения на производительность фиксируемых
объектов. Они записываются для всех лет расчетного периода, на протяжении
которых производительность соответствующего объекта считается заданной и имеют
форму равенства (для объектов, со строго фиксированной производительностью),
или двусторонних ограничений, если производительность объекта задается
интервалом значений. В обоих случаях в качестве правой части ограничений
принимается производительность (![]() ) данного объекта (k) в рассматриваемом
варианте, которая задается или последовательностью дискретных значений по годам
расчетного периода, или нижними и верхними границами допустимой области
изменения.
) данного объекта (k) в рассматриваемом
варианте, которая задается или последовательностью дискретных значений по годам
расчетного периода, или нижними и верхними границами допустимой области
изменения.
Второе дополнение, необходимое для
превращения обычной модели в адаптивную, — введение новых переменных,
характеризующих возможные «подстроечные» мероприятия.
Состав этих мероприятий подбирается
таким образом, чтобы с их помощью удавалось компенсировать возможные диспропорции
во всех уравнениях модели. Производственные характеристики этих мероприятий и
особенности их использования на разных этапах расчетного периода описываются, в
модели с помощью дополнительной матрицы технологических коэффициентов (![]() ) и специальных ограничений на отдельные «подстроечные» переменные или их сумму. Удельные же затраты
на «подстроечные» мероприятия учитываются в виде
дополнительных коэффициентов функционала (
) и специальных ограничений на отдельные «подстроечные» переменные или их сумму. Удельные же затраты
на «подстроечные» мероприятия учитываются в виде
дополнительных коэффициентов функционала (![]() ) при новых переменных.
) при новых переменных.
В построенную таким образом адаптивную
модель последовательно подставляются заранее заготовленные сочетания исходных
данных — коэффициенты вектора ограничений (![]() ).
).
Это могут быть как ранее найденные N
сочетаний исходных данных, так и полученное па их основе меньшее число
сочетаний, описывающих динамику условии развития системы с учетом процесса
уточнения исходной информации.
Рассмотренная - модификация адаптивной
модели представляет собой общую задачу линейного программирования с заданным
набором векторов ограничений. Ее решение одним из методов корректировки оптимального
базиса позволяет найти лучшие способы приспособления заданного варианта к
каждому рассматриваемому сочетанию исходных данных и суммарные затраты на
развитие и адаптацию системы.
Особенности принятия
решений по развитию экономических систем в условиях неопределенности
Конечной целью планирования
экономических систем является выбор наилучшего варианта ее развития. При этом
решающую роль играет критерий выбора.
Традиционный критерий минимума
приведенных затрат позволяет выявить зону неопределенности оптимального
развития системы. Для сравнения же вариантов в пределах этой зоны его
целесообразно модифицировать в критерий минимума экономического ущерба. Однако
каждый вариант характеризуется не одним, а совокупностью (N) значений
экономического ущерба — по числу рассмотренных условий развития системы.
Возникает вопрос, какой именно параметр кривой распределения значений
экономического ущерба целесообразно принять в качестве критерия сравнения
вариантов. В настоящее время имеется несколько мнений по этому вопросу [3]*.
В большинстве случаев лучшим оказывается
вариант, имеющий наименьшее среднее значение экономического ущерба, т. е.
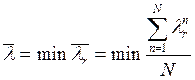 (1)
(1)
Но для уникальных экономических систем
(например, топливно-энергетического комплекса страны) наряду с этим важно
застраховаться и от слишком больших перерасходов затрат. Тогда для выбора
варианта рекомендуется критерий минимума максимального значения экономического
ущерба, т.е.
![]() (2)
(2)
Минимаксный критерий (2) ориентируется
только на худшие условия развития системы, при этом не учитывается поведение
системы в более благоприятных обстоятельствах.
Этот недостаток частично устраняется,
если искать решение в «смешанных стратегиях». Для этого достаточно представить
выбор окончательного решения в виде некоторой антагонистической игры двух лиц с
нулевой суммой, задаваемой платежной матрицей. Путем сведения игры к
соответствующей - задаче линейного программирования
![]() (3)
(3)
можно найти цену игры или, что то же
самое, минимальный гарантированный риск перерасхода затрат и «смешанный»
вариант развития системы.
«Смешанный» вариант является наилучшим
действием в случае возникновения любого из условий развития системы и
вычисляется как
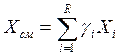
где ![]() - компоненты двойственного решения задачи (3) или доли
участия каждого варианта (Хi) в их выпуклой комбинации (Хсм).
- компоненты двойственного решения задачи (3) или доли
участия каждого варианта (Хi) в их выпуклой комбинации (Хсм).
Однако и этот вариант не является
идеальным решением, поскольку «игровой» подход предполагает активное
противодействие со стороны второго игрока (условий развития системы), но в
действительности же такая гипотеза неправомерна. Кроме того, сомнение вызывает
Целесообразность практической реализации «смешанного» варианта. Как о
правдоподобном способе развития системы речь может идти лишь в частном случае —
при одинаковой структуре (составе) существенных переменных вариантов,
участвующих в формировании «смешанного» способа развития системы.
Таким образом, ни один из рассмотренных
критериев не свободен от условностей и не может безоговорочно применяться при
оптимизации экономических систем. Но это отнюдь не свидетельствует о бесполезности
сложной и трудоемкой работы по экономической оценке и сравнению вариантов в
пределах зоны неопределенности. Напротив, выполненные в СЭИ исследования экспериментально подтвердили
необходимость такого анализа систем.
Таким образом, совместное применение
критериев принятия решения в условиях неопределенности не обеспечивает
получение единственного результата, а позволяет выявить лишь некоторую
(достаточно компактную) совокупность вариантов практически равноценных с точки
зрения экономических критериев. Такие варианты можно считать равноэкономичными.
Экономико-математический
анализ результатов решения
При решении задач прогнозирования
развития производственных систем методами линейного программирования для
матрицы, образующей базис оптимального плана, может быть получена обратная
матрица, которая, как и оценки оптимального плана, может быть использована для
целей экономико-математического анализа результатов решения таких задач.
Использование элементов обратной матрицы
позволяет:
а) определить допустимые пределы
изменения параметров ограничений задачи (лимитов по ресурсам, мощностям и
размеров потребностей), в которых система оценок оптимального плана остается
неизменной. Выявление интервалов устойчивости оценок позволяет целенаправленно
подойти к изменению условий задачи (уровня потребности продукции или лимитов,
выделяемых для отрасли ресурсов), приводящих к повышению общей эффективности
плана (например, уменьшению суммарных затрат) без повторных пересчетов всей
задачи;
б) определить частичные изменения плана
(интенсивности, применяемых способов производства и транспортировки продукции)
при некоторых изменениях параметров ограничений. Это позволяет без повторных
пересчетов всей задачи определить последствия (изменения плана) частичных
вынужденных или желаемых изменений в лимитах выделяемых ресурсов или размерах
потребности в продукции отрасли;
в) определить структуру полных затрат на
производство продукции внутри отрасли путем разложения оценок продуктов на их
составляющие: прямые затраты и затраты обратной связи, которые представляют
собой изменения прямых затрат по выпуску других продуктов в связи с
использованием дефицитных ресурсов в производстве данного продукта.
Обозначим
через D базисную матрицу оптимального
решения задачи. Каков смысл коэффициентов
обратной матрицы? Воспользуемся формулой
![]() [4] т. е.
[4] т. е. 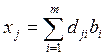 . Таким образом,
каждая компонента вектора
. Таким образом,
каждая компонента вектора ![]() определяется как
произведение соответствующей строки коэффициентов обратной
матрицы на вектор правых частей ограничений. Строка обратной матрицы в данном случае выступает связующим звеном между значением компоненты вектора
определяется как
произведение соответствующей строки коэффициентов обратной
матрицы на вектор правых частей ограничений. Строка обратной матрицы в данном случае выступает связующим звеном между значением компоненты вектора ![]() и значением
компонент вектора правых частей ограничений
и значением
компонент вектора правых частей ограничений ![]() . При изменении какой-либо компоненты вектора
. При изменении какой-либо компоненты вектора ![]() на единицу значение компонент вектора
на единицу значение компонент вектора ![]() изменяется па величину соответствующих коэффициентов
изменяется па величину соответствующих коэффициентов ![]() . Направление изменения значения будет определяться знаком
. Направление изменения значения будет определяться знаком ![]() и знаком bi . При
этом имеется в виду изменение
и знаком bi . При
этом имеется в виду изменение ![]() , допустимое
в пределах базиса оптимального решения.
, допустимое
в пределах базиса оптимального решения.
Таким образом, коэффициенты ![]() показывают влияние
каждой единицы правой части соответствующего ограничения
на значение компонент вектора
показывают влияние
каждой единицы правой части соответствующего ограничения
на значение компонент вектора ![]() в оптимальном плане. Если
взять i-й столбец коэффициентов dji, то он
будет характеризовать влияние i-гo ограничения на значение всех компонент вектора
в оптимальном плане. Если
взять i-й столбец коэффициентов dji, то он
будет характеризовать влияние i-гo ограничения на значение всех компонент вектора ![]() . Равенство некоторых
. Равенство некоторых
![]() нулю означает, что соответствующее ограничение не влияет
на величину интенсивности использования j-го способа.
нулю означает, что соответствующее ограничение не влияет
на величину интенсивности использования j-го способа.
Таким образом, если был определен оптимальный план ![]() , то при увеличении bi на
, то при увеличении bi на ![]() новый план
будет:
новый план
будет:
![]()
т. е. к исходному оптимальному плану нужно прибавить соответствующий
столбец коэффициентов замещения подматрицы
симплексной таблицы. При таком изменении
вектора ![]() значение целевой функции увеличивается на величину оценки этого ограничения.
значение целевой функции увеличивается на величину оценки этого ограничения.
Однако
обратная матрица оптимального решения позволяет
установить связь не только между вектором правых частей ограничений и значениями базисных компонент искомого плана, но
и между коэффициентами целевой функции
и значениями оценок ограничений, т. е. с
помощью обратной матрицы можно выяснить структуру оценок. В оптимальном плане
для базисных векторов выполняется
соотношение ![]() , следовательно,
, следовательно, 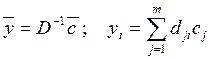
Таким образом, с помощью обратной матрицы можно представить оценки ограничений в виде линейной функции от
прямых затрат.
Один из важнейших аспектов анализа оптимального решения
— определение допустимой области изменения исходных
данных, в пределах которой при любом сочетании исходных данных сохранялась бы оптимальность полученного плана.
Для этого проводится анализ устойчивости
оптимального базиса и соответствующей ему системы о. о. оценок при
изменении внешних параметров модели: правых частей ограничений, коэффициентов
целевой функции, коэффициентов производственных способов. Интервалы устойчивости оптимального решения могут определяться
при изменении одного параметра модели (все
остальные параметры зафиксированы), при одновременном изменении нескольких исходных параметров, при одновременном изменении многих исходных
параметров (например, всех
коэффициентов целевой функции и всех
правых частей ограничений).
Нахождение таких интервалов устойчивости необходимо для того, чтобы определить, как «ведет» себя модель при некоторых изменениях исходных данных. А это очень важно для формулирования требований к точности исходных
данных, для частичного изменения в нужном направлении
получаемой извне информации, для уточнения самой модели.
Нужно
заметить, что под анализом устойчивости понимается
и исследование решения при изменение структуры модели: типа критерия,
количества и состав ограничений. В этом
случае устойчивость плана определяется на
основе серии расчетов. Так, при решении отраслевых задач на минимум приведенных затрат можно, анализируя оптимальный план, провести дополнительные расчеты
при других критериях оптимальности, например, минимуме текущих затрат, минимуме капитальных вложений и т. д. Эти расчеты, как отмечалось, дают возможность
выявить объекты оптимизируемой системы, эффективность которых бесспорна.
Выявлению степени устойчивости части плана
способствуют расчеты задачи и при изменении состава и количества
ограничений. Например, в отраслевых задачах
часто ставятся ограничения на интенсивность
использования способов производства в
оптимальном плане вида 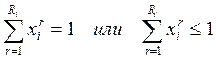
(для
всех предприятий или только для некоторых из них). Ограничения первого типа оказывают наиболее сильное влияние на формирование оптимального плана и
значение целевой функции, так как область свободы выбора резко сужается. Если часть первых условий или все заменить на условие необязательного включения предприятий в план (т. е. на второе условие), то
сразу же выявятся предприятия, входящие устойчиво в план отрасли, т. е. являющиеся наиболее эффективными. Обычно
при замене первых условий на вторые
из плана выпадает часть действующих предприятий, по которым проводится
дополнительный экономический анализ.
Какие-либо выводы о степени устойчивости оптимального
плана при изменении структуры модели можно сделать лишь при рассмотрении
конкретной задачи в зависимости от ее
особенностей.
Ниже рассматриваются основные подходы к нахождению
интервалов устойчивости оптимального плана, получаемого в результате решения задачи, которая сведена к общей задаче линейного программирования. В данном случае
речь пойдет не о вариантных расчетах, которые, конечно, очень важны, а об анализе интервалов устойчивости одного варианта плана, т. е. такой анализ
может сочетаться с вариантными расчетами
и может быть применен как на
последнем их шаге, так и в ходе расчетов. Если же дополнительные расчеты не
'производятся, тем более важно проанализировать интервалы устойчивости полученного плана в отношении частичного изменения
внешних параметров оптимизируемой
отраслевой системы. Рассмотрим отдельные случаи изменения исходных
параметров и анализа влияния этих изменений на оптимальное решение.
1. Изменяется только один параметр модели — коэффициент
целевой функции, а остальные зафиксированы прежнем
уровне. Необходимые для расчетов формулы можно вывести на основе
свойств симплекс-метода и исходя из условий устойчивости оптимального базиса и неотрицательности (переменных:
а) Интервалы устойчивости для
![]() при небазисных
переменных можно определить исходя из того, чтобы не нарушался признак оптимальности плана, иначе говоря, должно выполняться:
при небазисных
переменных можно определить исходя из того, чтобы не нарушался признак оптимальности плана, иначе говоря, должно выполняться:
![]() т.е.
т.е.
![]() откуда
откуда
![]()
Таким образом, для небазисных переменных показатель целевой функции ![]() может быть увеличен неограниченно, что не приведет к изменению оптимального плана (так как это только ухудшает эффективность не вошедших в базис способов). Пределом уменьшения
может быть увеличен неограниченно, что не приведет к изменению оптимального плана (так как это только ухудшает эффективность не вошедших в базис способов). Пределом уменьшения ![]() является величина
оценки введения в базис j-го способа
является величина
оценки введения в базис j-го способа ![]() , так как при
, так как при ![]() оценка этого способа станет равной нулю
оценка этого способа станет равной нулю ![]() , и следовательно, этот способ может войти в оптимальный план, а
базис измениться.
, и следовательно, этот способ может войти в оптимальный план, а
базис измениться.
б) Интервалы
устойчивости для ![]() при базисных переменных можно найти также на основе признака
оптимальности плана.
при базисных переменных можно найти также на основе признака
оптимальности плана.
Пусть коэффициент целевой функции при i-й базисной переменной получает
приращение ![]() . Тогда косвенные эффекты
всех небазисных переменных изменяются на величину
. Тогда косвенные эффекты
всех небазисных переменных изменяются на величину ![]() , что в свою
очередь приведет к изменению значений оценок небазисных способов. Оценки станут равными
, что в свою
очередь приведет к изменению значений оценок небазисных способов. Оценки станут равными ![]() . Для того
чтобы не изменился оптимальный базис,
должно выполняться
. Для того
чтобы не изменился оптимальный базис,
должно выполняться ![]() . Отсюда
. Отсюда
![]() , т. е.
, т. е.
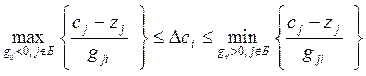
Следовательно, в качестве границ интервалов нужно взять соответственно максимальное и минимальное отношение оценок способов к отрицательным или положительным коэффициентам замещения симплексной таблицы.
2. Одновременно получают приращение все коэффициенты
целевой функции (при неизменности других параметров
модели). Тогда условие неизменности оптимального базиса запишется так:
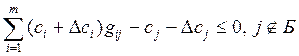
или
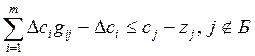
Следовательно,
определение допустимых интервалов изменения
коэффициентов ![]() при неизменности других параметров модели сводится к решению системы неравенств указанного вида. При этом в случае большой
размерности задачи может потребоваться
большой объем вычислений. Наиболее
целесообразно в практических расчетах
заранее задавать структуру изменения коэффициентов целевой функции, т. е. задавать вектор
при неизменности других параметров модели сводится к решению системы неравенств указанного вида. При этом в случае большой
размерности задачи может потребоваться
большой объем вычислений. Наиболее
целесообразно в практических расчетах
заранее задавать структуру изменения коэффициентов целевой функции, т. е. задавать вектор ![]() , который характеризует предполагаемые типы
изменения вектора
, который характеризует предполагаемые типы
изменения вектора ![]() . В этом случае нахождение допустимых интервалов изменения коэффициентов
. В этом случае нахождение допустимых интервалов изменения коэффициентов ![]() сводится к нахождению критического значения параметра задачи параметрического
программирования.
сводится к нахождению критического значения параметра задачи параметрического
программирования.
В результате несложных преобразований определяются
интервалы устойчивости для ![]() .
.
![]()
где
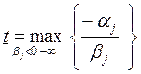
если все ![]() ;
;
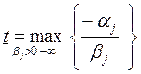
если все ![]() ;
;
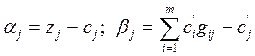 .
.
Если предположить, что ![]() есть единичный орт с 1 на s- м месте, то эти формулы превращаются в частные формулы для нахождения допустимого приращения одного коэффициента cs (при неизменности всех остальных).
есть единичный орт с 1 на s- м месте, то эти формулы превращаются в частные формулы для нахождения допустимого приращения одного коэффициента cs (при неизменности всех остальных).
3. Определение допустимых интервалов изменения правых частей ограничений, для которых остаются
неизменными оценки оптимального плана.
а) Изменяется только одна, например, j-я компонента
вектора ![]() (при
неизменности всех остальных). Тогда пределы варьирования компонент вектора
(при
неизменности всех остальных). Тогда пределы варьирования компонент вектора ![]() можно определить
исходя из условия неотрицательности переменных в оптимальном
плане, т. е. должно всегда выполняться:
можно определить
исходя из условия неотрицательности переменных в оптимальном
плане, т. е. должно всегда выполняться:
![]() , где {
, где {![]() } — оптимальный план задачи;
} — оптимальный план задачи;
![]() — приращение i-й базисной переменной
при изменении
вектора
— приращение i-й базисной переменной
при изменении
вектора ![]() . Если
. Если ![]() изменяется на
изменяется на ![]() , то
, то ![]()
(![]() — элемент обратной
матрицы оптимального решения). Тогда условие устойчивости оптимального базиса запишется так:
— элемент обратной
матрицы оптимального решения). Тогда условие устойчивости оптимального базиса запишется так:
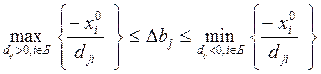 .
.
б) Одновременно изменяются все
компоненты вектора правых частей ограничений (при неизменности других параметров
модели).
Допустимые
приращения ограничений ![]() будут
определяться системой неравенств
будут
определяться системой неравенств
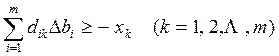 .
.
Здесь также
практически целесообразно задавать вектор ![]() , характеризующий -предполагаемые
типы изменения вектора
, характеризующий -предполагаемые
типы изменения вектора ![]() . Тогда можно перейти к задаче параметрического
программирования и определить искомые интервалы следующим образом:
. Тогда можно перейти к задаче параметрического
программирования и определить искомые интервалы следующим образом:
![]() где
где
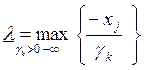
если все ![]() ,
,
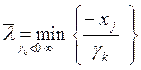
если все ![]() ,
,
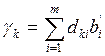 .
.
Если вектор ![]() есть
единичный орт с 1 на l-м месте,
то эти формулы превращаются в формулы для нахождения интервала устойчивости
одной l-й компоненты вектора
есть
единичный орт с 1 на l-м месте,
то эти формулы превращаются в формулы для нахождения интервала устойчивости
одной l-й компоненты вектора ![]() , которые рассматривались выше.
, которые рассматривались выше.
Большое значение
для практики имеет одновременное изменение в экономических задачах показателей
затрат и компонентов вектора правых частей ограничений. В книге «Оптимальное
территориально-производственное планирование» (Новосибирск, «Наука», 1969)
рассматривается 6 групп изменений правых частей ограничений, и исследуются
целесообразность и экономический смысл тех или иных изменений в ограничениях по
продукции и ресурсам. Рассмотрение различных случаев нахождения интервалов
устойчивости для коэффициентов целевой функции и вектора правых частей
ограничений позволяет сделать вывод, что в математическом отношении эти расчеты
несложны. Однако при практическом применнии этой
методики возникает проблема определения векторов с' и V, т. е. определения
характера изменения всех компонент векторов ![]() и
и ![]() . Другими словами, нужно определить заранее структуру
возможных изменений затрат и потребности в .продукции
и лимитов по ресурсам в отраслевой задаче, что является само по себе непростой
экономической проблемой.
. Другими словами, нужно определить заранее структуру
возможных изменений затрат и потребности в .продукции
и лимитов по ресурсам в отраслевой задаче, что является само по себе непростой
экономической проблемой.
Простейшие схемы формирования
экономической оценки лесных ресурсов.
Рассмотрим систему, состоящую из трех
лесных участков, на которых заготовка кубометра обезличенной древесины требует
соответственно 15, 14.5, 13 единиц совокупных затрат (для определенности будем
говорить о приведенных затратах в рублях на 1 м3). Расчетная
лесосека (максимально возможный объем заготовки) составляет по участкам 600,
700, и 300 м3, а требуется заготовить 1100 м3. Очевидно,
если исходить из критерия минимума затрат, то необходимо полностью использовать
второй и третий участки, а на первом заготавливать 100 м3. Суммарные
приведенные затраты в этом случае составляют 15550 руб.
В случае сокращения расчетной лесосеки
третьего участка до 299 м3 на первом участке будет заготавливаться
101 м3, а суммарные затраты возрастут на 2 руб. – разница между
затратами на заготовку выбывающей и замещающей единиц ресурса.
При замещении единицы ресурса второго
участка на единицу первого такой показатель будет равен 0.5 руб.
В нашем примере замещающим является
ресурс с замыкающими затратами на заготовку. Но если ввести в задачу
дополнительные условия, замещающим может быть другой ресурс. Например, пусть
необходимо полностью использовать первый участок (очистка ложа водохранилища и
т.п.). Тогда план заготовок по участкам будет соответственно 600, 200, и 300м3,
а суммарные затраты составят 15800 руб. Изъятие единицы ресурса на третьем
участке приведет к увеличению суммарных затрат на 1.5 руб., т.к. будет
компенсироваться ростом заготовок на втором участке, а не на третьем. Этот
прирост затрат связанный с замещением ресурса в оптимальном плане, определяет
экономическую оценку источника ресурса в выделенной локальной системе.
Нашему примеру соответствует простейшая
линейная модель использования лесных ресурсов.
Введем обозначения.
i – индекс лесоучастка, ![]() (I – множество
всех индексов участков);
(I – множество
всех индексов участков);
Ni -
расчетная
лесосека по i му участку;
ci –
совокупные
затраты на заготовку кубометра древесины на
i – м участке;
П
– общая
потребность в заготовленной древесине;
xi – искомый объем
заготовок на i- м участке;
Тогда модель запишется следующим
образом:
![]() (1)
(1)
-
на каждом участке может быть заготовлено древесины не больше расчетной лесосеки;
![]() (2)
(2)
-
потребность в древесине должна быть удовлетворена
![]() (3)
(3)
-
совокупные затраты должны быть минимальными.
Этой задаче соответствует двойственная
задача:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Где
v – объективно обусловленная (о.о.) оценка продукции;
ui – о.о.
оценка i - го лесоучастка.
Для вошедших в оптимальный план способов
лесозаготовок выполняется равенство
![]() ,
а для замещающего источника
,
а для замещающего источника ![]() . В связи с этим оценка продукции (v) равна затратам
на заготовку в замещающем участке, а о.о. оценки лесоучастков носят рентный характер. В
ситуациях, когда построение оптимального плана не вызывает затруднений,
нахождение замещающего ресурса является простой задачей. В более усложненных
случаях можно воспользоваться простым примером.
. В связи с этим оценка продукции (v) равна затратам
на заготовку в замещающем участке, а о.о. оценки лесоучастков носят рентный характер. В
ситуациях, когда построение оптимального плана не вызывает затруднений,
нахождение замещающего ресурса является простой задачей. В более усложненных
случаях можно воспользоваться простым примером.
При решении задач линейного
программирования для матрицы коэффициентов технологических способов, образующих
базис оптимального плана, может быть получена соответствующая обратная матрица.
Использование элементов обратной матрицы
позволяет,
во–первых, изменение плана при
«небольших» вариациях вектора ограничений;
во–вторых, найти структуру объективно
обусловленных оценок путем разложения на прямые затраты и затраты обратной
связи.
Каждая компонента вектора решения определяется умножением строки коэффициентов
обратной матрицы на вектор ограничений. Следовательно, при изменении какой либо
компоненты вектора ограничений на единицу оптимальное решение задачи меняется
на величину соответствующих компонент столбца обратной матрицы, а коэффициенты
строки показывают изменение величины о. о. оценок при варьировании прямых затрат (коэффициентов
целевой функции). Последнее означает. что с помощью обратной матрицы можно
представить, в частности о.о. оценки ресурсов в виде
линейной функции от прямых затрат.
Проанализируем обратные матрицы
оптимального базиса для простейших моделей использования ресурса. Введем
обозначения для строк и столбцов прямой и обратной матрицы:
Xi
– i- столбец исходной матрицы
коэффициентов;
Pi
- i- строка исходной матрицы для ресурсов;
Пi - i- строка
исходной матрицы для продукции;
DПi, DPi - соответственно отрицательный
или положительный орт, вводимый для приведения
i – й строки к
равенству.
Исходная матрица (первоначальная
симплекс-таблица) будет выглядеть следующим образом:
|
|
X1 |
X2 |
X3 |
DР1 |
DР2 |
DР3 |
DП1 |
|
Правая часть |
|
1 участок |
1 |
|
|
1 |
|
|
|
= |
600 |
|
2 участок |
|
1 |
|
|
1 |
|
|
= |
700 |
|
3участок |
|
|
1 |
|
|
1 |
|
= |
300 |
|
Потребление |
1 |
1 |
1 |
|
|
|
-1 |
= |
1100 |
|
Коэф-ты
целевой функции |
15 |
14,5 |
13 |
0 |
0 |
0 |
0 |
à |
min |
Обратную матрицу будем для наглядности
окаймлять решением прямой и двойственной задач, значениями правых частей и
коэффициентов целевой функции. Для первой исходной ситуации обратная матрица
представлена в таблице 1.
Таблица 1 Матрица связей о. о. оценок и основных факторов.
|
Столбцы матрицы |
Коэф-ты целевой
функции |
Объемы ресурсов |
Объем |
Значения переменных в опт. плане |
||
|
Р1=600 |
Р2=700 |
Р3=300 |
П1=1100 |
|||
|
X1 |
15 |
|
-1 |
-1 |
1 |
100 |
|
X2 |
14,5 |
|
1 |
|
|
700 |
|
X3 |
13 |
|
|
1 |
|
300 |
|
DР1 |
0 |
1 |
1 |
1 |
-1 |
500 |
|
О. о. оценки |
0 |
-0,5 |
-2 |
15 |
|
|
|
|
|
|
|
|
|
|
Знак и величина о.о.
оценки показывают, к какому изменению затрат приводит увеличение на единицу
соответствующей компоненты вектора ограничений.
Как указывалось выше о. о. оценка
ресурсов в этом случае получается как разность затрат на заготовку между
оцениваемым и замещающим ресурсом, при этом изменение затрат на заготовку по
первому лесоучастку ведет к изменению почти всей системы о. о. оценок.
Введение дополнительного условия по
обязательному использованию всех ресурсов первого участка приводит к
видоизменению матрицы (см. табл. 2).
Здесь особо следует остановиться на
оценке ограничения по расчетной лесосеке для первого участка.
Таблица
2 Матрица связей о. о. оценок и основных факторов (при обязательном использовании
всех ресурсов на первом участке).
|
Столбцы |
Коэф-ты целевой
функции |
Объемы ресурсов |
Объем |
Значения переменных |
||
|
матрицы |
Р1=600 |
Р2=700 |
Р3=300 |
П1=1100 |
в опт. плане |
|
|
X1 |
15 |
1 |
|
|
|
600 |
|
X2 |
14,5 |
-1 |
|
-1 |
1 |
200 |
|
X3 |
13 |
|
|
1 |
|
300 |
|
DР2 |
0 |
1 |
1 |
1 |
-1 |
500 |
|
О.о. оценки |
0,5 |
0 |
-1,5 |
14,5 |
|
|
Оценка 0,5 руб./м3 показывает
величину «излишних» затрат, связанных с обязательной эксплуатацией экономически
неэффективного (с точки зрения учтенных в системе условий) источника. В этом
примере замещающим является второй участок, и по отношению к нему
рассчитывается экономическая оценка (дифференциальная рента), которая для
первого участка может трактоваться как необходимая компенсация затрат системы.
Элементы обратной матрицы имеют очевидный экономический смысл и не требуют
специального разъяснения.
Структура обратной матрицы будет более
сложной в случае учета качества ресурса. Учтем деление заготавливаемой
древесины на деловую и дровяную, и в дополнение к условиям, принятым в первой
ситуации пусть требуется заготовить 1000м3 деловой и 100 м3 дровяной
древесины. Доля деловой древесины по участкам соответственно составляет 70, 65,
и 77% от заготавливаемой, а остальную часть составляет дровяная. Если
обозначить через аij – выход j – го вида
древесины (![]() ) при заготовке одного кубометра обезличенной древесины
на i – м участке; Пj – общую потребность в j – м виде, то модель запишется следующим образом:
) при заготовке одного кубометра обезличенной древесины
на i – м участке; Пj – общую потребность в j – м виде, то модель запишется следующим образом:
![]() (7)
(7)
- ограничение по расчетной лесосеке;
![]() (8)
(8)
- ограничение по удовлетворению
потребности в каждом виде древесины;
![]() (9)
(9)
- совокупные затраты должны быть
минимальными.
Исходная матрица (первоначальная
симплекс-таблица) будет выглядеть следующим образом:
|
|
X1 |
X2 |
X3 |
DР1 |
DР2 |
DР3 |
DП1 |
DП2 |
|
Правая часть |
|
1 участок |
1 |
|
|
1 |
|
|
|
|
= |
600 |
|
2 участок |
|
1 |
|
|
1 |
|
|
|
= |
700 |
|
3участок |
|
|
1 |
|
|
1 |
|
|
= |
300 |
|
Потребление 1-го вида |
0,70 |
0,65 |
0,77 |
|
|
|
-1 |
|
= |
1000 |
|
Потребление 2-го вида |
0,30 |
0,35 |
0,23 |
|
|
|
|
-1 |
|
100 |
|
Коэф-ты
целевой функции |
15 |
14,5 |
13 |
0 |
0 |
0 |
0 |
|
à |
min |
Существенная диспропорция между заданной
структурой потребления и структурой заготовок предопределяет избыток дровяной
древесины. В этом случае замыкающий по затратам первый участок в связи с
большим выходом деловой древесины оказывается более эффективным, чем второй, и
используется полностью.
Обратная
матрица и решение пары двойственных задач приведены в таблице 3.
Таблица 3. Матрица связей о. о. оценок и
основных факторов с учетом качества ресурса (при дефиците одного продукта).
|
Столбцы |
Коэф-ты целевой
функции |
Объемы ресурсов |
Объем потребления продукции по видам |
Значения переменных |
|||
|
матрицы |
Р1=600 |
Р2=700 |
Р3=300 |
П1=600 |
П2=600 |
|
|
|
X1 |
15 |
1 |
0 |
0 |
0 |
0 |
600,0 |
|
X2 |
14,5 |
-1,08 |
0 |
-1,18 |
1,54 |
0 |
536,9 |
|
X3 |
13 |
0 |
0 |
1 |
0 |
0 |
300,0 |
|
DР2 |
0 |
1,08 |
1 |
1,18 |
-1,54 |
0 |
163,1 |
|
DП2 |
0 |
-0,08 |
0 |
-0,18 |
0,54 |
-1 |
336,9 |
|
О.о. оценки |
-0,62 |
0 |
-4,18 |
22,31 |
0 |
|
|
Существенная диспропорция между заданной
структурой потребления и структурой заготовок предопределяет избыток дровяной
древесины. В этом случае замыкающий по затратам первый участок в связи с
большим выходом деловой древесины оказывается более эффективным, чем второй, и
используется полностью.
Отметим,
что увеличение потребности в деловой древесине на единицу повлечет
необходимость увеличить заготовки на втором участке на величину 1/0,65=1, 538 м3,
а затраты вырастут на 1,538 * 14, 5 =
22,31 руб. Возможность заготовок дополнительной единицы на третьем участке
привела бы к сокращению заготовок на втором участке на 0,77/0,65=1,185 м3
и уменьшению затрат на 1,185*14,5-13,0=4,177 руб., что является экономической
оценкой третьего участка в данной системе. Аналогичное рассуждение можно
провести относительно о. о. оценки первого участка, равной 0,7/0,65*14,5-15=0,615
руб. Здесь расчет замыкающего участка ведется с учетом качественных
характеристик. В случае дефицитности одного продукта легко определить
коэффициенты замещения ресурсов и соответствующую экономию затрат при интенсивном
использовании эффективных источников ресурса.
Комментарии к отчету об
устойчивости MS-Excel
Влияние изменения запаса ресурсов (правых
частей ограничений)
1. Отчет
Excel об устойчивости включает таблицу "Ограничения" и в ней колонку "Теневая цена" (Shadow Price). Теневые цены – это решение Yi двойственной задачи (объективно обусловленные оценки).
Они показывают, как меняется целевая функция при малом изменении bi:
![]() .
.
2. Эти
оценки верны только в пределах устойчивости решения, т.е. пока
изменение bi не изменяет угловую точку области допустимых решений, в которой достигается максимум целевой функции (при этом численные
значения переменных решениях, конечно,
изменяются). При выходе bi за пределы устойчивости теневые
цены изменятся.
3.
Пределы изменения bi ,в которых оптимальное решение соответствует той же самой угловой точке, также даны в
таблице "Ограничения" ("Допустимое
увеличение" и "Допустимое уменьшение").
a)
Причем если ресурс используется полностью
(дефицитный),
существует как верхний, так и нижний предел.
b)
Если же ресурс используется не полностью,
верхний предел устойчивости равен бесконечности (Excel пишет 1Е+30, что означает
10+30, максимально известное программе число).
4.
Следует понимать, что пределы устойчивости для изменения bi. даются при условии, что все остальные значения правых частей bk (при k ≠ i) остаются неизменными. Одновременное изменение двух и более коэффициентов (bi и bк), каждого внутри своего
интервала устойчивости, может привести к изменению теневых цен.
Влияние
изменений в коэффициентах целевой функции (в
терминах задачи максимизации)
1.
Изменение коэффициентов целевой функции Cj не изменяет вида области допустимых решений.
Оно изменяет наклон семейства прямых, изображающих целевую функцию.
2. До
тех пор пока изменение наклона не превышает некоторых пределов, оптимальное
решение {Xj} вообще не меняется (максимальное значение
целевой функции при этом, конечно, меняется).
3. При
выходе значений коэффициента целевой функции за эти пределы решение скачком
перемещается в другую угловую точку области допустимых решений (при этом
решение {Xj} может измениться очень сильно).
"Допустимое
увеличение" и "Допустимое уменьшение" для каждого коэффициента
целевой функции c, при которых оптимальное решение не
изменяется, приведены в таблице "Изменяемые ячейки" отчета Excel об
устойчивости.
a) Причем если Xj > 0 (продукт входит в оптимальный план), то имеется
как верхний, так и нижний предел для изменения соответствующего j-го коэффициента целевой функции.
b) Если же Хj = 0, то "Допустимое уменьшение" может быть
как угодно велико - продукт все равно не войдет в оптимальный план. Верхний
предел "Допустимое увеличение" показывает, насколько нужно увеличить
соответствующий целевой коэффициент, чтобы j-й
продукт вошел в оптимальный план.
c) Величина,
противоположная этому увеличению, называется Нормированная стоимость (Reduced Cost) и
показывает, на сколько нынешняя цена продукта ниже приемлемой цены (или
издержки выше замыкающих – при решении задачи на минимум), при которой j-й продукт может войти в оптимальный план.
5.
Следует понимать, что пределы устойчивости для изменения Сj даются
при условии, что значения всех остальных целевых коэффициентов Ск
(при k ≠ j ) остаются
неизменными. Одновременное изменение двух и более коэффициентов (сj и ск), каждого
внутри своего интервала устойчивости, может привести к изменению оптимального
решения.
Моделирование
конкретных ситуаций. Экономические постановки задач.
Ситуация 1. Обоснование плана
добычи и переработки нефти;
Рассматриваемая система состоит из трех нефтедобывающих районов, двух
нефтеперерабатывающих заводов (НП1, НП2) и двух
районов потребления (P1, P2). На каждом из заводов нефть может перерабатываться по двум технологиям с
выходом двух продуктов (светлые и темные).
Известно, что первый
нефтедобывающий район может поставлять сырую нефть на оба завода и имеет
задание по вывозу за пределы рассматриваемой системы (в размере 200 млн.т.). Второй район также имеет задание по вывозу (70 млн.т.) и может поставлять нефть на первый завод. Третий
район может поставлять нефть только на второй завод. Приведенные затраты на
транспортировку нефти от пунктов добычи к пунктам переработки даны в табл. 1.
Таблица 1. Приведенные затраты на транспортировку нефти
к пунктам переработки (у.е./т.)-
|
|
НП1 |
НП2 |
|
НД1 |
2 |
22 |
|
НД2 |
4 |
|
|
НД3 |
|
1 |
Технологические способы переработки на нефтеперерабатывающих заводах характеризуются
нормой выхода нефтепродуктов с одной тонны сырой нефти и показателями затрат на
переработку. Их различие заключается в степени глубины переработки нефти.
Характеристика способов приведена в табл.2.
Таблица 2. Характеристика способов переработки нефти.
|
|
НП1 |
НП2 |
||
|
|
1 способ |
2 способ |
1 способ |
2 способ |
|
Выход светлых нефтепродуктов на 1 т.
нефти (т) |
0,42 |
0,74 |
0,42 |
0,74 |
|
Выход темных нефтепродуктов на 1 т.
нефти (т) |
0,53 |
0,08 |
0,53 |
0,08 |
|
Приведенные затраты на переработку 1т.
нефти (у.е.) |
6 |
11 |
9 |
15 |
Распределение потребности в нефтепродуктах по районам дано в табл.3.
Таблица 3. Потребность в нефтепродуктах по районам (млн.т.)
|
|
Нефтепродукты |
|
|
|
светлые |
темные |
|
Р1 |
40 |
30 |
|
Р2 |
15 |
10 |
Транспортная схема допускает перевозку продукции первого завода в
оба района, а второго - только во второй район. Показатели затрат в табл.4.
Таблица 4. Удельные затраты на перевозку нефтепродуктов потребителям (у.е./т.)
|
Заводы |
Районы |
|
|
Р1 |
Р2 |
|
|
|
светлые |
|
|
НП1 |
2 |
20 |
|
НП2 |
- |
1,5 |
|
|
темные |
|
|
НП1 |
1 |
19 |
|
НП2 |
|
0,5 |
Промышленные запасы нефти во всех районах рассчитаны на десятилетний период
эксплуатации месторождений с равномерным темпом отбора. Величина запасов и
коэффициенты извлекаемости нефти приведены в табл.5.
Таблица 5. Технико-экономические
показатели добычи нефти по районам
|
Показатели |
Районы нефтедобычи |
||
|
НД1 |
НД2 |
НД3 |
|
|
Запасы (млн. т.) |
6250 |
2400 |
300 |
|
Коэффициент извлечения |
0,4 |
0,5 |
0,5 |
|
Приведенные затраты на
подготовку запасов (у.е. /т. запасов) |
1 |
2 |
3 |
|
Приведенные затраты на
добычу нефти (у.е. /т.) |
11 |
18 |
22 |
Требуется определить
оптимальный план добычи, переработки и транспортировки нефти и нефтепродуктов
по критерию минимизации суммарных приведенных затрат и провести
экономико-математический анализ получаемого решения
ОБОСНОВАНИЕ.ПЛАНА ДОБЫЧИ И ПЕРЕРАБОТКИ НЕФТИ;
Примем, что рассматриваемая система состоит из трех
нефтедобывающих районов двух нефтеперерабатывающих заводов (НП1, НП2) и Двух
районов потребления (P1, P2). На каждом из заводов нефть может перерабатываться по двум
технологиям с выходом двух продуктов (светлые и темные).
Известно, что первый
нефтедобывающий район может поставлять сырую нефть на оба завода и имеет
задание по вывозу за пределы рассматриваемой системы (в размере 200 млн.т.). Второй район также имеет задание по вывозу (70 млн.т.) и может поставлять нефть на первый завод. Третий
район может поставлять нефть только на второй завод. Приведенные затраты на
транспортировку нефти от пунктов добычи к пунктам переработки даны в табл. 1.
Таблица 1. Приведенные затраты на транспортировку нефти к пунктам
переработки (руб./т.)-
|
|
НП1 |
НП2 |
|
НД1 |
2 |
22 |
|
НД2 |
4 |
|
|
НД3 |
|
1 |
Технологические способы переработки на нефтеперерабатывающих заводах характеризуются
нормой выхода нефтепродуктов с одной тонны сырой нефти и показателями затрат на
переработку.: Их различие заключается в степени
глубины переработки нефти. Характеристика способов приведена в табл.2.
Таблица 2. Характеристика способов переработки нефти.
|
|
НП1 |
НП2 |
||
|
|
1 способ |
2 способ |
1 способ |
2 способ |
|
Выход
светлых нефтепродуктов на 1 т. нефти (т) |
0,42 |
0,74 |
0,42 |
0,74 |
|
Выход
темных нефтепродуктов на 1 т. нефти ; т) |
0,53 |
0,08 |
0,53 |
0,08 |
|
Приведенные
затраты на переработку 1т. нефти (руб.) |
6 |
11 |
9 |
15 |
Распределение потребности в нефтепродуктах по районам дано в
табл.3.
Таблица 3. Потребность в
нефтепродуктах по районам (млн.т.)
|
|
Нефтепродукты |
|
|
|
светлые |
темные |
|
Р1 |
40 |
30 |
|
Р2 |
15 |
10 |
Транспортная схема допускает перевез продукции первого
завода в оба района, а второго - только во второй район. Показатели затрат в
табл.4.
Таблица 4. Удельные затраты на перевозку нефтепродуктов
потребителям (руб./т.)
|
Заводы |
Районы |
|
|
Р1 |
Р2 |
|
|
|
светлые |
|
|
НП1 |
2 |
20 |
|
НП2 |
- |
1,5 |
|
|
темные |
|
|
НП1 |
1 |
19 |
|
НП2 |
|
0,5 |
Промышленные
запасы нефти во всех районах рассчитаны не десятилетний период эксплуатации
месторождений с равномерным темпом отбора. Величина запасов и коэффициенты извлекаемости нефти приведены в табл.5.
Таблица 5. Технико-экономические показатели добычи нефти по
районам
|
Показатели |
•районы нефтедобычи |
||
|
НД1 |
НД2 |
НД3 |
|
|
Запасы
(млн. т.) |
6250 |
2400 |
300 |
|
коэффициент
извлечения |
0,4 |
0,5 |
0,5 |
|
приведенные
затраты на подготовку запасов (руб. /т.) |
1 |
2 |
3 |
|
приведенные
затраты на добычу нефти (руб. /т.) |
11 |
18 |
22 |
Требуется
определить оптимальный план добычи, переработки и транспортировки нефти и
нефтепродуктов по критерию минимизации суммарных приведенных затрат и провести
экономико-математический анализ получаемого решения
Оптимизация
лесопользования в НСО
Новосибирская область относится к
малолесным районам (на ее долю приходится немногим более 2%: общего запаса древесины Западной Сибири). Пространственно
леса области произрастают в Северной (таежные леса), Центральной (Присалаирские леса) и Южной (Сузунские
леса) зонах. С учетом климаторегулирующих, водоохранных и почвозащитных функций
леса и условий его восстановления максимально возможный годовой объем
лесозаготовок составляет в Северной зоне 600
тыс. м3, в Центральной - 700
тыс. м3, Южной - 300 тыс. м3.
Качественный состав и условия
лесозаготовок по зонам различны. Выход деловой древесины при заготовке одного
обезличенного кубометра и требуемые при этом приведенные затраты по каждой зоне
даны в таблице 2.1.
Таблица 2.1 Технико-экономические
показатели лесозаготовок
|
Показатели |
Един. |
Зоны |
||
|
Северная |
Центральная |
Южная |
||
|
Выход
деловой древесины |
% |
70 |
65 |
77 |
|
Затраты
на заготовку |
у.е./ м3 |
13.5 |
14 |
12.5 |
Заготовленная в Северной и Центральной
зонах древесина вывозится в хлыстах (ствол дерева без кроны) в Новосибирск, а
древесина, заготовленная в Южной зоне - в
Сузун. Транспортные затраты на перевозку одного кубометра обезличенной древесины
составляют для: Северной зоны - 2 у.е.,
Центральной - 0,5 у.е., Южной - 0,5 у.е. В Новосибирске и Сузуне может быть
организована переработка ввозимой древесины на пиломатериалы и
древесностружечные плиты. Современная технология такова, что для производства 1 м3 пиломатериалов требуется 1,6 м3 древесины деловой и при этом
образуется 0,3 м3
утилизируемых твердых отходов, а для производства 1 м3 древесностружечных плит требуется 1,5 м3 дровяной древесины или
твердых отходов.
Затраты на
переработку различаются по пунктам производства и видам конечной продукции (см.
табл.2.2).
Таблица 2.2 Приведенные затраты на переработку
лесосырья
(у.е./ м3 конечной продукции)
|
Виды
конечной продукции переработки |
Новосибирск |
Сузун |
|
Пиломатериалы |
20 |
22 |
|
Древесностружечные
плиты из дров |
40 |
43 |
|
Древесностружечные
плиты из отходов |
38 |
41.5 |
Деловая древесина, пиломатериалы и
древесностружечные плиты могут ввозиться в Новосибирск из Сузуна и
Красноярского края. В первом случае транспортные затраты на перевозку
составляют: для деловой древесины - 2,5
у.е./м3 для пиломатериалов -2,1
у.е./м3 , а для плит - 2,6
у.е./м3. Во втором случае суммарные приведенные
производственно-транспортные затраты (франко-пункт-потребления) составляют: для
деловой древесины -20,7у.е./м3
для пиломатериалов - 51,5 у.е./м3 а для плит - 47,5 у.е./м3.
Основные потребители лесопродукции
сконцентрированы в двух городах: Новосибирске и Сузуне. Рассчитайте вариант
удовлетворения фиксированного спроса (таблица 2.3).
Таблица 2.3 Фиксированные
годовые объемы потребления лесопродукции.
|
Наименование
продукции |
Ед.
измер. |
Новосибирск |
Сузун |
|
Деловая
древесина |
тыс.
м3 |
150 |
30 |
|
Дрова |
-/- |
45 |
25 |
|
Пиломатериалы |
-/- |
700 |
50 |
|
Древесностружечные
плиты |
-/- |
200 |
20 |
Ситуация
3а. Оптимальный выбор потребителя.
Предположим, что в Новосибирске 500 тыс. м3 пиломатериалов и 150 тыс. м3 ДСП реализуется через
несвязанные контракты. Максимальные объемы по каждому контракту (в тыс. м3)
и соответствующие цены (в тыс. у.е.) приведены в таблице 2.4.
Таблица 2.4.
|
|
Пиломатериалы |
ДСП |
||
|
Мах объем |
Цена за ед. |
Мах объем |
Цена за ед. |
|
|
1-ый
контракт |
150 |
53.0 |
40 |
50.0 |
|
2-ой
контракт |
130 |
52.5 |
30 |
47.0 |
|
3-ий
контракт |
100 |
52.0 |
30 |
46.0 |
|
4-ый
контракт |
80 |
51.5 |
25 |
45.5 |
|
5-ый
контракт |
40 |
51.3 |
25 |
45.0 |
Ситуация 3.
Оптимизация лесопользования с учетом сезонности
В Северной
зоне НСО лесозаготовки ведутся на зимней (слабые грунты не позволяют тяжелой
технике проводить там заготовку древесины в летний период) и летней лесосеках.
Максимально возможный объем лесозаготовок за сезон составляет на зимней
лесосеке - 300 тыс. м3, а
летней - 70 тыс. м3.
Качественный состав и условия лесозаготовок по зонам
различны. Выход деловой древесины при заготовке одного обезличенного кубометра
и требуемые при этом приведенные затраты по каждой лесосеке даны в таблице 3.1.
Таблица 3.1 Технико-экономические показатели лесозаготовок
|
|
Един. |
Лесосеки |
|||
|
|
Зимняя |
Летняя |
||||
|
Выход
деловой древесины |
% |
80 |
55 |
||
|
Затраты на
заготовку |
у.е./ м3 |
16.5 |
14 |
||
Заготовленная
на зимней лесосеке древесина может быть продана или переработана на
пиломатериалы и древесностружечные плиты. Кроме того, заготовленная деловая
древесина может быть сохранена для переработки в летний период (затраты на
хранения составляют, по периодам, 1.0 у.е./ м3 и 0.5 у.е./ м3).
Потери при межсезонном хранении могут достигать 10%. В летний период на
реализацию и переработку может быть направлена как заготавливаемая, так и
сохраненная с предыдущего периода древесина.
Современная
технология такова, что для производства 1
м3 пиломатериалов требуется 1,6
м3 деловой древесины и при этом образуется 0,3 м3 утилизируемых твердых отходов (которые могут
быть проданы или переработаны), а для производства 1 м3 древесностружечных плит (ДСП) требуется 1,5 м3 дровяной древесины или
твердых отходов.
Затраты на переработку (у.е./м3
конечной продукции):
Производство пиломатериалов - 20;
Производство ДСП из дров - 40;
Производство ДСП из отходов - 38.
Максимальные
объемы реализации (прогнозируемый спрос) и цены по сезонам отличаются. Оплата
продаваемых дров и отходов производится единовременно в полном объеме, а
реализация деловой древесины, пиломатериалов и ДСП допускает дебиторскую
задолженность (на один сезон) до 20%. Соответствующие цены и объемы приведены в
таблице 3.2. Внерыночное потребление распределено на две равные доли по
сезонам.
Таблица 3.2 Максимальные объемы и цены реализации, у.е./м3
|
Виды продукции |
зимний период |
летний период |
Внерыночное
потребление |
||
|
объем |
цена |
объем |
цена |
||
|
Деловая древесина |
15 |
20.5 |
20 |
21.5 |
20 |
|
Дрова |
15 |
2.5 |
20 |
2 |
4 |
|
Отходы |
15 |
2 |
20 |
1 |
2 |
|
Пиломатериалы |
30 |
75 |
70 |
78 |
10 |
|
ДСП |
30 |
70 |
70 |
72 |
10 |
По каждому
периоду должен соблюдаться баланс между доходами и расходами. Учитывая
сезонность лесозаготовок, есть необходимость привлечения заемных средств под
достаточно высокий процент – 20%, с требованием возврата денег в следующем
периоде. Остаток средств с предыдущего года составляет
15 тыс. у.е., а минимальный запас финансовых средств на конец рассматриваемого
цикла должен составлять не менее 10 тыс.
у.е.
В качестве
целевой функции предлагается рассматривать условную прибыль – разность межу
доходами от реализации продукции и затратами.
Моделирование
развития электроэнергетики района
В районе прогнозируется развитие
энергообеспечения хозяйства. Дополнительная потребность в электроэнергии может
быть удовлетворена за счет передачи из единой энергосистемы и строительства
электростанций на месте. Проектировщики считают возможным строительство в
районе электростанций трех типов: гидравлических, тепловых и атомных. Для
каждого из них разработано по три взаимоисключающих варианта строительства.
Технико-экономические показатели вариантов приведены в таблицах 1 - 3.
Таблица
1. Технико-экономические показатели строительства гидравлических электростанций
(ГЭС).
|
Показатели |
Единица измерения |
Варианты |
||
|
1 |
2 |
3 |
||
|
Установленная
мощность |
млн
кВт |
0,3 |
0,5 |
0,625 |
|
Время
использования мощности |
час/год |
5000 |
4000 |
4000 |
|
Капитальные
вложения |
млрд руб. |
4,0 |
5,0 |
5,5 |
|
Себестоимость
электроэнергии |
коп/кВтч |
10 |
9 |
8 |
Таблица
2. Технико-экономические показатели строительства тепловых электростанций
(ТЭС).
|
Показатели |
Единица измерения |
Варианты |
||
|
1 |
2 |
3 |
||
|
Установленная
мощность |
млн кВт |
0,25 |
0,4 |
0,48 |
|
Время
использования мощности |
час/год |
8000 |
6250 |
6250 |
|
Капитальные
вложения |
млрд руб. |
1,4 |
2,25 |
3,30 |
|
Себестоимость
электроэнергии |
коп/кВтч |
27,5 |
21,0 |
15,3 |
|
Годовые
затраты на охрану природы |
млн руб |
20 |
150 |
320 |
Таблица
3. Технико-экономические показатели строительства атомных электростанций (АЭС).
|
Показатели |
Единица измерения |
Варианты |
||
|
1 |
2 |
3 |
||
|
Установленная
мощность |
млн кВт |
0,2 |
0,24 |
0,32 |
|
Время
использования мощности |
час/год |
5000 |
6250 |
6250 |
|
Капитальные
вложения |
млрд руб. |
2,0 |
3,15 |
4,0 |
|
Себестоимость
электроэнергии |
коп/кВтч |
20,0 |
17,0 |
16,0 |
Предполагается, что из единой
энергосистемы может быть получено не более 1 млрд кВтч
электроэнергии в год стоимостью 45,0 коп./кВтч, при
этом потребуется 1,2 млрд руб. капиталовложений на строительство линии
электропередач (ЛЭП).
Необходимо определить показатели программы развития энергообеспечения
района при следующих условиях.
По первому сценарию потребность в
электроэнергии составляет 4.5 млрд. кВтч, а на реализацию программы строительства выделяется
6,9 млрд. руб, по второму сценарию потребность в
электроэнергии может составить 4 млрд. кВтч, а на
строительство будет выделено 5,8 млрд. руб., по третьему сценарию,
соответственно, 5 млрд кВтч и 7,8 млрд. руб.
Определить стратегию развития
электроэнергетики региона с минимальным экономическим ущербом, вызванным
возможной ошибкой прогноза, при измерении ущерба в текущих затратах. В качестве
подстроечного мероприятия может рассматриваться консервация строительства
станций. Потери капиталовложений, связанные с консервацией объектов, приведены
в таблице 4.
Таблица
4. Потери капиталовложений, связанные с консервацией строительства электростанций,
млн. руб
|
Тип станции |
Варианты |
||
|
1 |
2 |
3 |
|
|
ГЭС
|
400 |
500 |
800 |
|
ТЭС
|
100 |
250 |
500 |
|
АЭС
|
150 |
300 |
500 |
Какая
стратегия развития энергетики является предпочтительной с позиции минимизации
экономического ущерба?
Рекомендуемая литература
1.
Методические
положения оптимального отраслевого планирования в промышленности Новосибирск
издательство «Наука»1972
2.
Перспективное
отраслевое планирование: экономико-математические методы и модели /Новосибирск
издательство «Наука»1986г.
3.
Казакевич
Д.М. Производственно - транспортные модели в
перспективном отраслевом планировании/ Экономика Москва - 1972
4.
Планирование
отраслевых систем /Экономика Москва - 1974
5.
Природные
ресурсы в моделях территориально – производственных систем Новосибирск,
«Наука»1982г.
6.
Джеффри
Мур, Ларри Р. Уэдерфорд
Экономическое моделирование в Microsoft Office Excel:
пер. с англ. М.: Издательский дом «Вильямс»,2004.
7.
Таха Х.А. Введение в
исследование операций. М.: Издательский дом «Вильямс», 2001
8.
Блам
Ю. Ш., Машкина Л. В. Введение в линейную оптимизацию: Методическое пособие.
Новосибирск: НГУ, 1999.
9.
Блам
Ю. Ш., Машкина Л. В. Введение оптимизацию (простейшие задачи линейного
программирования), методическое пособие. Новосибирск: НГУ, 1997.
10.
Задачник
- практикум по оптимальному отраслевому планированию. Учебное пособие. НГУ,
1982.
11.
Акулич И. Л.
Математическое программирование в примерах и задачах Москва «высшая школа»,
1993.
12.
Зайцев М.
Г. Методы оптимизации управления для менеджеров
13.
Васильков Ю. В.,
Василькова Н. Н. Компьютерные технологии вычислений в математическом
моделировании. — М.: Финансы и статистика, 2001.
14.
Исследование операций в экономике / Под ред.
Н. Ш. Кремера. — М.: ЮНИТИ, 2004.
15.
Пантелеев А. В., Летова Т. А.
Методы оптимизации в примерах и задачах. — М.: Высш.
шк., 2002.
16.
Курицкий Б. Я. Поиск
оптимальных решений средствами Excel 7.0. — СПб.: BHV – Санкт Петербург, 1997.
17.
Бахтин А. Е. Математическое моделирование в
экономике. — Н.: НГАЭиУ, 1995.
18.
Гранберг А. Г. Моделирование социалистической
экономики. — М.: Экономика, 1988.
19.
Моисеев Н. Н. Математика ставит эксперимент. — М.:
Наука, 1979.
20.
Хуторецкий А. Б. Модели исследования операций
Новосибирск 2006.
21.
Интрилигатор М. математические методы оптимизации и экономическая теория. М.:
Айрис-пресс,2002.
22.
Полищук Л. И. Анализ многокритериальных экономико-математических
моделей. Новосибирск: Наука, 1989.
23.
Шмырев В. И. Лекции по математическому программированию. Новосибирск: НГУ,
2000.
24.
Беллман Р., Дрейфус С. Прикладные задачи
динамического программирования. – М.: Наука 1965.
25.
Беллман Р. Динамическое программирование. – М.:
Иностранная литература, 1965.
Оглавление
Производственно-транспортные
модели
Оптимизация
в условиях неопределенности
Экономико-математический
анализ результатов решения
Комментарии
к "Отчету по устойчивости" MS EXCEL
Моделирование
конкретных ситуаций: